题目内容
19.下列代数式$\frac{1}{5}$(1-x),$\frac{1}{π}$,$\frac{{{x^2}-{y^2}}}{3}$,$\frac{1}{m}$+m,$\frac{{5{a^2}}}{2a}$,$\frac{5}{6+x}$中是分式的有( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解答 解:$\frac{1}{5}$(1-x),$\frac{1}{π}$,$\frac{{{x^2}-{y^2}}}{3}$的分母中均不含有字母,因此它们是整式,而不是分式.
$\frac{1}{m}$+m,$\frac{{5{a^2}}}{2a}$,$\frac{5}{6+x}$分母中含有字母,因此是分式.
故选:C.
点评 本题主要考查分式的定义,注意π不是字母,是常数,所以$\frac{1}{π}$不是分式,是整式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
11.将方程x2+4x+1=0配方后得到的形式是( )
| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+4)2=-3 | D. | (x+4)2=3 |
 如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2.
如图,将边长为2的正方形ABCD沿对角线AC平移至正方形A1B1C1D1,当重叠部分面积为2时,则正方形ABCD平移的距离AA1=2$\sqrt{2}$-2. 折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则EC=3.
折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则EC=3.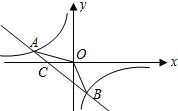 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点. 如图,⊙O的直径CD⊥弦EF,垂足为点G,∠EOD=58°,则∠F=61°.
如图,⊙O的直径CD⊥弦EF,垂足为点G,∠EOD=58°,则∠F=61°.