题目内容
 如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧
如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧 | BC |
分析:因为∠BDA和∠BCA为同弧所对的圆周角,所以相等,又AC为直径,所以∠ABC=90°,即∠ACB+∠BAC=90°,又∠BAP=∠BDA,所以∠BAP+∠BAC=90°,即AP为切线.
解答:解:∠BDA和∠BCA为同弧所对的圆周角,
∴∠BDA=∠BCA.
又AC为直径,
∴∠ABC=90°.
即∠ACB+∠BAC=90°.
又∠BAP=∠BDA,
∴∠BAP+∠BAC=90°.
即AP为切线.
∴∠BDA=∠BCA.
又AC为直径,
∴∠ABC=90°.
即∠ACB+∠BAC=90°.
又∠BAP=∠BDA,
∴∠BAP+∠BAC=90°.
即AP为切线.
点评:此题综合考查了切线的判定以及相似三角形的判定方法的运用,解题的关键是利用90°的圆周角所对的弦是直径判定圆内最长的弦.

练习册系列答案
相关题目
 如图,半圆的直径AB=10cm,弦AC=6cm,把AC沿直线AD对折恰好与AB重合,则AD的长为( )
如图,半圆的直径AB=10cm,弦AC=6cm,把AC沿直线AD对折恰好与AB重合,则AD的长为( )A、4
| ||
B、3
| ||
C、5
| ||
| D、8cm |
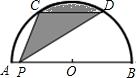 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于 如图,半圆的直径AB=10,点C在半圆上,BC=6.
如图,半圆的直径AB=10,点C在半圆上,BC=6.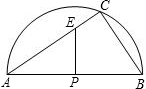 如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6.
如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6. 秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.
秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.