题目内容
(2012•江干区一模)如图,半圆的直径AB=2,点C从点A向点B沿着半圆运动,速度为每秒
,运动时间为t( 秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.
秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.
(1)如果OC∥BD,求t的值及
的值;
(2)当t=3时,求
的值.
| π |
| 6 |
 秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.
秒),D是弧BC的中点,连接AD,BC相交于点E,连接BD.(1)如果OC∥BD,求t的值及
| BD |
| AE |
(2)当t=3时,求
| BD |
| AE |
分析:(1)求出∠DBC=∠C=∠CBA=30°,求出弧AC长,即可求出t,求出DB、AD、DE,AE,代入即可求出答案;
(2)过E作EF⊥AB于F,求出AC、BC,求出BF、EF,求出AE,证△ACE∽△BDE,得出
=
,推出DB=
,代入求出即可.
(2)过E作EF⊥AB于F,求出AC、BC,求出BF、EF,求出AE,证△ACE∽△BDE,得出
| DB |
| AC |
| BE |
| AE |
| AC•BE |
| AE |
解答: 解:(1)∵OC∥DB,OB=OC,
解:(1)∵OC∥DB,OB=OC,
∴∠DBC=∠C=∠CBA,
∴弧DC=弧AC,
又∵点D平分弧BC,
∴弧DC=弧AC=弧BD,
∴∠DBC=∠C=∠CBA=30°,
∴弧AC=
π,
∴t=
π÷
=2.
∵在Rt△ABD中,∠D=90°,AB=2,
∴DB=1,AD=
.
∵在Rt△BDE中,∠D=90°,BD=1,∠DBE=30°,
∴tan30°=
,
∴DE=
,
∴AE=
,
∴
=
;
(2)解: 过点E作EF⊥AB于点F,
过点E作EF⊥AB于点F,
∵当t=3时,弧AC=
π,∠ABC=45°,
∵EF⊥AB,
∴∠EFB=90°,
∴∠BEF=45°=∠CBA=∠CAB,
∵∠C=90°,
∴AC=BC=
,BF=EF=CE=2-
,EB=
BF=2
-2,
∴AE2=(
)2+(2-
)2=8-4
,
∵AB为直径,
∴∠C=∠D=90°,
∵∠AEC=∠BED,
∴△ACE∽△BDE,
∴
=
,
∴DB=
,
∴
=
=
=
.
 解:(1)∵OC∥DB,OB=OC,
解:(1)∵OC∥DB,OB=OC,∴∠DBC=∠C=∠CBA,
∴弧DC=弧AC,
又∵点D平分弧BC,
∴弧DC=弧AC=弧BD,
∴∠DBC=∠C=∠CBA=30°,
∴弧AC=
| 1 |
| 3 |
∴t=
| 1 |
| 3 |
| π |
| 6 |
∵在Rt△ABD中,∠D=90°,AB=2,
∴DB=1,AD=
| 3 |
∵在Rt△BDE中,∠D=90°,BD=1,∠DBE=30°,
∴tan30°=
| DE |
| BD |
∴DE=
| 1 |
| 3 |
| 3 |
∴AE=
| 2 |
| 3 |
| 3 |
∴
| DB |
| AE |
| ||
| 2 |
(2)解:
 过点E作EF⊥AB于点F,
过点E作EF⊥AB于点F,∵当t=3时,弧AC=
| 1 |
| 2 |
∵EF⊥AB,
∴∠EFB=90°,
∴∠BEF=45°=∠CBA=∠CAB,
∵∠C=90°,
∴AC=BC=
| 2 |
| 2 |
| 2 |
| 2 |
∴AE2=(
| 2 |
| 2 |
| 2 |
∵AB为直径,
∴∠C=∠D=90°,
∵∠AEC=∠BED,
∴△ACE∽△BDE,
∴
| DB |
| AC |
| BE |
| AE |
∴DB=
| AC•BE |
| AE |
∴
| DB |
| AE |
| AC•BE |
| AE2 |
| ||||
8-4
|
| 1 |
| 2 |
点评:本题考查了相似三角形的性质和判定,平行线性质,含30度角的直角三角形,勾股定理的应用,主要考查学生运用定理进行推理的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
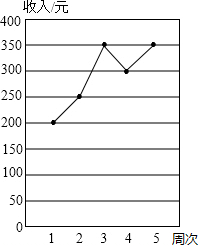 (2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( )
(2012•江干区一模)暑假里,小红参加了为期5周的勤工俭学活动,各周的收入情况如右图所示,以下结论中与右图反应的信息不相符的是( ) (2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )
(2012•江干区一模)将矩形ABCD沿EF折叠,使点B与AD上的点B'重合,如BE=4,AB'=3,则BF的长为( )