题目内容
 如图,半圆的直径AB=10,点C在半圆上,BC=6.
如图,半圆的直径AB=10,点C在半圆上,BC=6.(1)求弦AC的长;
(2)若P为AB的中点,PE⊥AB交AC于点E,求PE的长.
分析:AB是半圆的直径,点C在半圆上,∠ACB=90°,在直角△ABC中根据勾股定理就得到AC的长,易证△AEP∽△ABC,根据相似三角形的对应边的比相等,就可以求出PE的长.
解答:解:(1)∵AB是半圆的直径,点C在半圆上,
∴∠ACB=90°.
在Rt△ABC中,AC=
=
=8.
(2)∵PE⊥AB,
∴∠APE=90°.
∵∠ACB=90°,
∴∠APE=∠ACB.
又∵∠PAE=∠CAB,
∴△AEP∽△ABC.
∴
=
.
∴
=
.
∴PE=
=
.
∴∠ACB=90°.
在Rt△ABC中,AC=
| AB2-BC2 |
| 102-62 |
(2)∵PE⊥AB,
∴∠APE=90°.
∵∠ACB=90°,
∴∠APE=∠ACB.
又∵∠PAE=∠CAB,
∴△AEP∽△ABC.
∴
| PE |
| BC |
| AP |
| AC |
∴
| PE |
| 6 |
10×
| ||
| 8 |
∴PE=
| 30 |
| 8 |
| 15 |
| 4 |
点评:本题主要考查了直径所对的圆周角是直角,并且本题还考查了相似三角形的性质,对应边的比相等.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
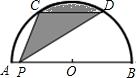 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于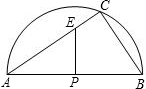 如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6.
如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6. (1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y=
(1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y= 如图,半圆的直径AB=10,点C在半圆上,BC=6.
如图,半圆的直径AB=10,点C在半圆上,BC=6. 如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )
如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )