题目内容
20.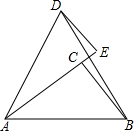 如图,△ABD为等边三角形,△ACB为等腰三角形且∠ACB=90°,DE⊥AC交AC的延长线于点E,求证:DE=CE.
如图,△ABD为等边三角形,△ACB为等腰三角形且∠ACB=90°,DE⊥AC交AC的延长线于点E,求证:DE=CE.
分析 连接CD,根据SSS定理得出△ACD≌△BCD(SSS),故∠ADC=∠BDC=30°.再求出∠DAC和∠DCE的度数,根据DE⊥AC可得出∠CDE=∠DCE=45°,故可得出结论.
解答  证明:连接CD,
证明:连接CD,
在△ACD与△BCD中,
∵$\left\{\begin{array}{l}CA=CB\\ DA=DB\\ DC=DC\end{array}\right.$
∴△ACD≌△BCD(SSS),
∴∠ADC=∠BDC=30°.
∵∠DAC=60°-45°=15°,
∴∠DCE=30°+15°=45°.
∵DE⊥AC.
∴∠CDE=∠DCE=45°,
∴DE=CE.
点评 本题考查的是全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
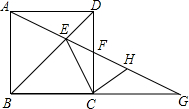 已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点.
已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点.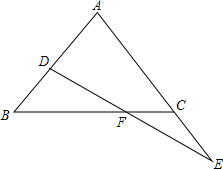 如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.
如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.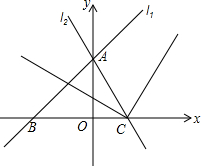 如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.
如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.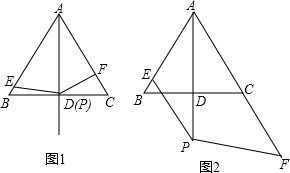

 如图是蕲春中轴线上的一座桥梁设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的直径为80m.
如图是蕲春中轴线上的一座桥梁设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的直径为80m.