题目内容
过多边形的一个顶点可以作7条对角线,则此多边形的内角和是外角和的( )
| A、4倍 | B、5倍 | C、6倍 | D、3倍 |
考点:多边形的对角线,多边形内角与外角
专题:
分析:从多边形一个顶点可作7条对角线,则这个多边形的边数是10,n边形的内角和可以表示成(n-2)•180°,代入公式就可以求出内角和,多边形的外角和为360°,相除即可.
解答:解:∵过多边形的一个顶点共有7条对角线,
故该多边形边数为10,
∴(10-2)•180°=1440°,
∴这个多边形的内角和为1440°,
又∵多边形的外角和为360°,
∴1440÷360=4.
故选:A.
故该多边形边数为10,
∴(10-2)•180°=1440°,
∴这个多边形的内角和为1440°,
又∵多边形的外角和为360°,
∴1440÷360=4.
故选:A.
点评:本题主要考查了多边形的对角线、内角和公式.外角和公式,是需要熟记的内容,比较简单.

练习册系列答案
相关题目
线段AB=5cm,BC=4cm,那么A、C两点的距离是( )
| A、1cm |
| B、9cm |
| C、1cm或9cm |
| D、以上答案都不对 |
 如图,AD∥EF∥BC,FG∥BD,和∠1相等的角有( )
如图,AD∥EF∥BC,FG∥BD,和∠1相等的角有( )| A、4个 | B、5个 | C、6个 | D、7个 |
 如图,与∠B是同旁内角的有( )
如图,与∠B是同旁内角的有( )| A、3个 | B、2个 | C、1个 | D、4个 |
若a>b,则下列不等式中不成立的是( )
| A、a-3>b-3 | ||||
| B、1-5a>1-5b | ||||
C、
| ||||
| D、-b>-a |
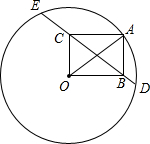 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于



 如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB边上的高,
如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB边上的高,