题目内容
11. 如图,在半径为4,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是4π-4.(结果保留π)
如图,在半径为4,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是4π-4.(结果保留π)
分析 根据BC为直径可知∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差.
解答 解:在Rt△ACB中,
∵AC=BC=4,
∴AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,
∵CD垂直平分AB,CD=BD=2$\sqrt{2}$,
∴D为半圆的中点,
S阴影部分=S扇形ACB-S△ADC=$\frac{1}{4}$π×42-$\frac{1}{2}$×(2$\sqrt{2}$)2=4π-4.
故答案为:4π-4.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
1. 如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
 如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P坐标为(-4,3),以点B(-1,0)为圆心,以BP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )| A. | -6和-5之间 | B. | -5和-4之间 | C. | -4和-3之间 | D. | -3和-2之间 |
6.一个罐头的质量为2.026kg,用四舍五入法将2.026kg精确到0.01kg 可得近似值( )
| A. | 2.03kg | B. | 2.02kg | C. | 2.0kg | D. | 2kg |
16.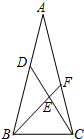 如图,在△ABC中,AB=AC,点D在边AB上,点E在线段CD上,且∠BEC=∠ACB,BE的延长线与边AC相交于点F,则与∠BDC相等的角是( )
如图,在△ABC中,AB=AC,点D在边AB上,点E在线段CD上,且∠BEC=∠ACB,BE的延长线与边AC相交于点F,则与∠BDC相等的角是( )
 如图,在△ABC中,AB=AC,点D在边AB上,点E在线段CD上,且∠BEC=∠ACB,BE的延长线与边AC相交于点F,则与∠BDC相等的角是( )
如图,在△ABC中,AB=AC,点D在边AB上,点E在线段CD上,且∠BEC=∠ACB,BE的延长线与边AC相交于点F,则与∠BDC相等的角是( )| A. | ∠DBE | B. | ∠CBE | C. | ∠BCE | D. | ∠A |
20.如图,该几何体的左视图是( )


| A. |  | B. |  | C. |  | D. |  |
 如图,在△ADC中,AD=BD=BC,∠C=30°,则∠ADB=60°.
如图,在△ADC中,AD=BD=BC,∠C=30°,则∠ADB=60°. 如图,CD是⊙O的直径,且CD=4cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.
如图,CD是⊙O的直径,且CD=4cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.