题目内容
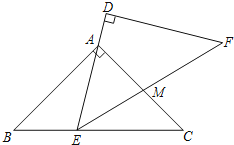
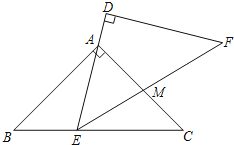
【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=![]() .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
【答案】2![]() ﹣
﹣![]() 或
或![]()
【解析】
分若AE=AM 则∠AME=∠AEM=45°;若AE=EM;若MA=ME 则∠MAE=∠AEM=45°三种情况讨论解答即可;
解:①若AE=AM 则∠AME=∠AEM=45°
∵∠C=45°
∴∠AME=∠C
又∵∠AME>∠C
∴这种情况不成立;
②若AE=EM
∵∠B=∠AEM=45°
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°
∴∠BAE=∠MEC
在△ABE和△ECM中,
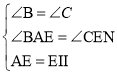 ,
,
∴△ABE≌△ECM(AAS),
∴CE=AB=![]() ,
,
∵AC=BC=![]() AB=2
AB=2![]() ,
,
∴BE=2![]() ﹣
﹣![]() ;
;
③若MA=ME 则∠MAE=∠AEM=45°
∵∠BAC=90°,
∴∠BAE=45°
∴AE平分∠BAC
∵AB=AC,
∴BE=![]() BC=
BC=![]() .
.
故答案为2![]() ﹣
﹣![]() 或
或![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目