题目内容
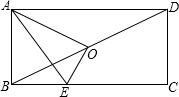 如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则
如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则 的值为
的值为
- A.

- B.

- C.

- D.8
A
分析:连接CO,由于O为长方形纸片ABCD的对称中心,得出A、O、C共线,AC是矩形的对角线,由折叠的性质可求得△ABC三边关系,得出∠ACB的度数,继而可求出 的值.
的值.
解答:连接CO,
∵O为长方形纸片ABCD的对称中心,
∴A、O、C共线,AC是矩形的对角线,
由折叠的性质知,AC=2AO=2AB=2b,
∴sin∠ACB= =1:2,
=1:2,
∴∠ACB=30°,
∴ =cot∠ACB=cot30°=
=cot∠ACB=cot30°= .
.
故选A.
点评:本题考查了折叠的性质,注意掌握折叠属于轴对称变换,根据轴对称的性质,折叠前后图形的形状和大小不变,对应边和对应角相等,难度一般.
分析:连接CO,由于O为长方形纸片ABCD的对称中心,得出A、O、C共线,AC是矩形的对角线,由折叠的性质可求得△ABC三边关系,得出∠ACB的度数,继而可求出
 的值.
的值.解答:连接CO,

∵O为长方形纸片ABCD的对称中心,
∴A、O、C共线,AC是矩形的对角线,
由折叠的性质知,AC=2AO=2AB=2b,
∴sin∠ACB=
 =1:2,
=1:2,∴∠ACB=30°,
∴
 =cot∠ACB=cot30°=
=cot∠ACB=cot30°= .
.故选A.
点评:本题考查了折叠的性质,注意掌握折叠属于轴对称变换,根据轴对称的性质,折叠前后图形的形状和大小不变,对应边和对应角相等,难度一般.

练习册系列答案
相关题目
 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
 如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则
如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则