Question

如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（　　）

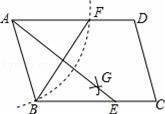
A．4       B．6       C．8       D．10

Answer 1

C【考点】平行四边形的性质；等腰三角形的判定与性质；勾股定理；作图—基本作图．

【专题】计算题．

【分析】由基本作图得到AB=AF，加上AO平分∠BAD，则根据等腰三角形的性质得到AO⊥BF，BO=FO=BF=3，再根据平行四边形的性质得AF∥BE，所以∠1=∠3，于是得到∠2=∠3，根据等腰三角形的判定得AB=EB，然后再根据等腰三角形的性质得到AO=OE，最后利用勾股定理计算出AO，从而得到AE的长．

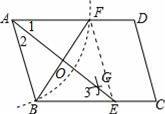
【解答】解：连结EF，AE与BF交于点O，如图，

∵AB=AF，AO平分∠BAD，

∴AO⊥BF，BO=FO=BF=3，

∵四边形ABCD为平行四边形，

∴AF∥BE，

∴∠1=∠3，

∴∠2=∠3，

∴AB=EB，

而BO⊥AE，

∴AO=OE，

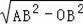
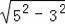
在Rt△AOB中，AO===4，

∴AE=2AO=8．

故选C．

【点评】本题考查了平行四边形的性质：平行四边形的对边相等；平行四边形的对角相等；平行四边形的对角线互相平分．也考查了等腰三角形的判定与性质和基本作图．