��Ŀ����
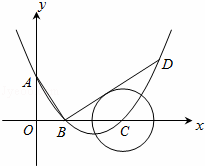
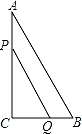
��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��﹣1���������߽�y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A������Ϊ��0��3����
��1����������ߵĽ���ʽ
��2������B���߶�AB�Ĵ��߽��������ڵ�D������Ե�CΪԲ�ĵ�Բ��ֱ��BD���У����ж������ߵĶԳ���l���C��������λ�ù�ϵ��������֤����
��3����֪��P���������ϵ�һ�����㣬��λ��A��C����֮��.�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������ʱP�������͡�PAC����������
�⣺��1����������Ϊy=a��x﹣4��2﹣1��
�������߾�����A��0��3����
��3=a��0﹣4��2﹣1�� ��··················2��
��··················2��
��������Ϊ ��····················3��
��····················3��
 ��2���ཻ��·······················4��
��2���ཻ��·······················4��
֤��������CE����CE��BD��
�� ʱ��x1=2��x2=6��
ʱ��x1=2��x2=6��
A��0��3����B��2��0����C��6��0����
�Գ���x=4��·························5��
��OB=2��AB= =
= ��BC=4��
��BC=4��
��AB��BD��
���OAB+��OBA=90�㣬��OBA+��EBC=90�㣬
���AOB�ס�BEC��
�� =
= ����
���� =
= �����CE=
�����CE= ��················6��
��················6��
�� ��2��
��2��
�������ߵĶԳ���l���C�ཻ��·····················7��
 ��3����ͼ������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
��3����ͼ������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
�����AC�Ľ���ʽΪ ��···················8��
��···················8��
��P���������m�� ����
����
��Q�������Ϊ��m�� ����················9��
����················9��
��PQ= m+3﹣��
m+3﹣�� m2﹣2m+3��=﹣
m2﹣2m+3��=﹣ m2+
m2+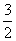 m��
m��
��S��PAC=S��PAQ+S��PCQ= ��﹣
��﹣ m2+
m2+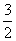 m����6
m����6
= ��m﹣3��2+
��m﹣3��2+ ��································11��
��································11��
�൱m=3ʱ����PAC��������Ϊ ��···················12��
��···················12��
��ʱ��P�������Ϊ��3�� ����·····················13��
����·····················13��

��1����������ð��������������ȫƵ���ֲ�ֱ��ͼ��
��2���ð��ί4���У�1��ѡ������2��ѡ������1��ѡ����������ʦҪ����4������ѡ2���˽����Ƕ�����ѡ�εĿ������������б�����״ͼ�ķ�������ѡ����2����ǡ��1��ѡ������1��ѡ������ĸ��ʣ�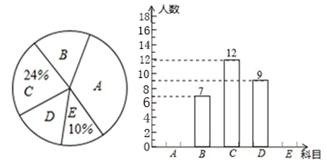
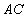 �ǵ���Բ��ֱ������
�ǵ���Բ��ֱ������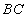 = 6cm����
= 6cm���� ��ĸ��
��ĸ�� =
=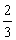
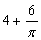 ��cm B��5cm C��
��cm B��5cm C�� cm D��7cm
cm D��7cm
 �Ľ���ǣ�������
�Ľ���ǣ������� B��
B�� C��﹣
C��﹣
 B��
B�� C��
C�� D��
D��
