题目内容
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人中恰好1人选修篮球,1人选修足球的概率.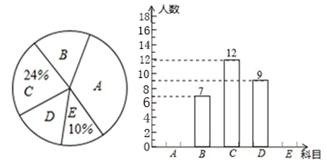
解:(1)该班总人数是:12÷24%=50(人),········1分
则E类人数是:50×10%=5(人),········2分
A类人数为:50﹣(7+12+9+5)=17(人).········3分
补全频数分布直方图如下:

·······························5分
(2)画树状图如下:

或列表如下:

······························9分
共有12种等可能的情况,恰好1人选修篮球,1人选修足球的有4种,
则概率是: =
= .·······················10分
.·······················10分

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 B.
B. C.
C. D.
D.

 B.
B. 
 D.
D. 
 .
.