题目内容
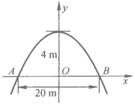
.有一座抛物线型拱桥(如图所示),正常水位时桥下河面宽20 m,河面距拱顶4 m. 试求:
(1)在如图26-10所示的平面直角坐标系中,求出抛物线解析式;
(2)为了保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水面在正常水位基础上涨多少米时,就会影响过往船只?
解:以点A为原点,以桌面中线为x轴,乒乓球水平运动方向为正方向,建立平面直角坐标系.
(1)由表格中的数据,可得当t为0.4时,乒乓球达到最大高度.
(2)由表格中的数据,可画出y关于x的图象,根据图象的形状,可判断y是x的二次函数.
可设y=a+0.45.
将(0,0.25)代入,可得a=-,∴ y=-+0.45.
当y=0时,=,=-(舍去),即乒乓球与端点A的水平距离是米.
(3)①由(2)得乒乓球落在桌面上时,对应的点为().
代入y=a得a+k=0,化简整理,得k=-
②由题意可知,扣杀路线在直线y=上.由①,得y= aa.
令a,整理,得20a-(120a+2)x+175a=0.
当Δ=-4×20a×175a=0时,符合题意.
解方程,得=,=.
当=时,求得x=-,不符合题意,舍去.
当=时,求得x=,符合题意.
答:当a=时,能恰好将球扣杀到点A.

练习册系列答案
相关题目
 和
和 ,那么点(
,那么点( 图象上的概率是 ( )
图象上的概率是 ( ) B.
B. C.
C. D.
D.

 的对称轴是直线 .
的对称轴是直线 . 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个 的值,使该抛物线与
的值,使该抛物线与 轴的一个交点在(1,0)和(3,0)之间,你所确定的
轴的一个交点在(1,0)和(3,0)之间,你所确定的
 。
。  ,则
,则 的值为_
的值为_ ________。
________。 ;
;  的图象开口向上,对称轴为直线x=-2,图象经过(1,0),下列结论中,正确的一项( )
的图象开口向上,对称轴为直线x=-2,图象经过(1,0),下列结论中,正确的一项( ) B.
B. 
 D.
D. 