题目内容
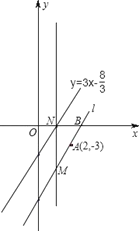
【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-![]() 平行.
平行.
(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-![]() 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
【答案】(1)直线l的解析式为y=3x9,B点坐标为(3,0);(2)P1(1,1),P2(1,2),P3(1, ![]() ).
).
【解析】
(1)设直线l的解析式为:y=kx+b,因为直线l与直线y=3x-![]() 平行,所以k=3,又直线l经过点A(2,-3),从而求出b的值,即可求出直线l的函数解析式及点B的坐标;
平行,所以k=3,又直线l经过点A(2,-3),从而求出b的值,即可求出直线l的函数解析式及点B的坐标;
(2)点M(a,-6)在直线l上,所以可先求出a的值,设点P(1,y),求出y的取值范围,再分情况讨论:当AB为斜边时,当PB为斜边时,当PA为斜边时,利用勾股定理建立方程求解即可.
解:(1)设直线l的解析式为y=kx+b(k≠0),
∵直线l平行于y=3x-![]() ,
,
∴k=3,
∵直线l经过点A(2,3),
∴3=3×2+b,b=9,
∴直线l的解析式为y=3x9,
当y=0时,x=3,
∴点B坐标为(3,0);
(2)∵点M(a,6)在直线l上,
∴3a-9=-6
∴a=1,则可设点P(1,y),
当x=1时,![]() =
=![]()
∴N(1,![]() ),
),
∴y的取值范围是6≤y≤![]() ,
,
∵P(1,y),A(2,-3),B (3,0)
∴![]() ,
,
![]()
![]()
当AB为斜边时,PA2+PB2=AB2,即![]() ,
,
整理得![]() ,解得y1=1,y2=2,
,解得y1=1,y2=2,
∴P1(1,1),P2(1,2),
当PB为斜边时,PA2+AB2=PB2,![]() ,
,
解得![]() ,
,
∴P3(1, ![]() ),
),
当PA为斜边时,PB2+AB2=PA2,即![]() ,
,
解得y=![]() ,
,
∵6≤y≤![]() ,故y=
,故y=![]() 不符合题意,舍去.
不符合题意,舍去.
∴综上所述,点P的坐标为P1(1,1),P2(1,2),P3(1, ![]() ).
).






