题目内容
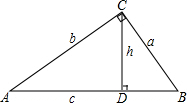 (1)如图,CD⊥AB,若BC=6,AC=8,AB=10,证明△ABC是直角三角形,并求CD.
(1)如图,CD⊥AB,若BC=6,AC=8,AB=10,证明△ABC是直角三角形,并求CD.(2)如图,Rt△ABC中,∠ACB=90°,CD⊥AB,若BC=a,AC=b,AB=c,CD=h,求证:
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
考点:勾股定理的逆定理,勾股定理
专题:
分析:(1)先由勾股定理的逆定理证明△ABC是直角三角形,再根据△ABC的面积不变列式求出CD;
(2)先在Rt△ABC中由勾股定理得出a2+b2=c2,再根据△ABC的面积不变列式得出ab=ch,进而证明
+
=
.
(2)先在Rt△ABC中由勾股定理得出a2+b2=c2,再根据△ABC的面积不变列式得出ab=ch,进而证明
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
解答:解:(1)∵△ABC中,BC=6,AC=8,AB=10,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
∵CD⊥AB,
∴△ABC的面积=
AB•CD=
AC•BC,
∴CD=
=
=4.8;
(2)∵Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,
∴a2+b2=c2.
∵CD⊥AB,
∴△ABC的面积=
ab=
ch,
∴ab=ch,
∴a2•b2=c2•h2,
∴
=
,
∴
=
,
∴
+
=
.
∴BC2+AC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
∵CD⊥AB,
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| 8×6 |
| 10 |
(2)∵Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,
∴a2+b2=c2.
∵CD⊥AB,
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴ab=ch,
∴a2•b2=c2•h2,
∴
| c2 |
| a2b2 |
| 1 |
| h2 |
∴
| a2+b2 |
| a2b2 |
| 1 |
| h2 |
∴
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
点评:本题考查了勾股定理,勾股定理的逆定理及三角形的面积,难度适中.

练习册系列答案
相关题目

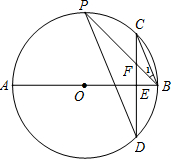 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C. 某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为