题目内容
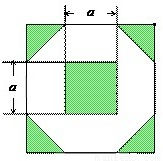
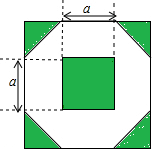 为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为2a2
2a2
.分析:△ABC是等腰直角三角形,斜边长是a,据此解求得△ABC的面积,则阴影部分的面积即可求解.
解答: 解:△ABC是等腰直角三角形,且AB=a,
解:△ABC是等腰直角三角形,且AB=a,
则AC=BC=
a,
则S△ABC=
AC•BC=
×
•
=
,
中间的正方形的面积是:a2,
则阴影部分的面积是:4×
+a2=2a2.
故答案是:2a2.
 解:△ABC是等腰直角三角形,且AB=a,
解:△ABC是等腰直角三角形,且AB=a,则AC=BC=
| ||
| 2 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
中间的正方形的面积是:a2,
则阴影部分的面积是:4×
| a2 |
| 4 |
故答案是:2a2.
点评:本题考查了正多边形的计算,正确求得三角形ABC的面积是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为![]() ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A.2![]() B. 3
B. 3![]() C. 4
C. 4![]() D.5
D.5![]()
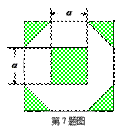
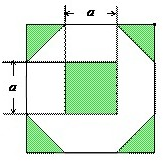 (2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )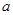 ,则阴影部分的面积为【 】
,则阴影部分的面积为【 】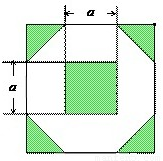
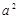 B. 3
B. 3