题目内容
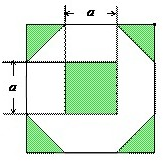（2012•安徽）为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为（ ）分析：根据正八边形的性质得出∠CAB=∠CBA=45°，进而得出AC=BC=
a，再利用正八边形周围四个三角形的特殊性得出阴影部分面积即可．
| ||
| 2 |
解答：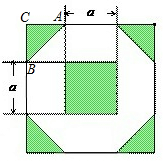
解：∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖，设正八边形与其内部小正方形的边长都为a，
∴AB=a，且∠CAB=∠CBA=45°，
∴sin45°=
=
=
，
∴AC=BC=
a，
∴S△ABC=
×
a×
a=
，
∴正八边形周围是四个全等三角形，面积和为：
×4=a2．
正八边形中间是边长为a的正方形，
∴阴影部分的面积为：a2+a2=2a2，
故选：A．
解：∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖，设正八边形与其内部小正方形的边长都为a，∴AB=a，且∠CAB=∠CBA=45°，
∴sin45°=
| BC |
| AB |
| BC |
| a |
| ||
| 2 |
∴AC=BC=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
∴正八边形周围是四个全等三角形，面积和为：
| a2 |
| 4 |
正八边形中间是边长为a的正方形，
∴阴影部分的面积为：a2+a2=2a2，
故选：A．
点评：此题主要考查了正八边形的性质以及等腰直角三角形的性质，根据已知得出S△ABC的值是解题关键．
练习册系列答案
相关题目
