题目内容
5.下面所给的四个图形中,其阴影部分面积等于2的图形是( )| A. |  | B. |  | C. |  | D. |  |
分析 先求出函数的图象和x轴、y轴的交点坐标,根据面积公式求出面积,再判断即可.
解答 解:A、阴影部分的面积S=$\frac{1}{2}×1×1+\frac{1}{2}×1×1$=1,故本选项不符合题意;
B、阴影部分的面积S=xy=1,故本选项不符合题意;
C、函数y=-x2+1的图象和y轴的交点坐标为(0,1),和x轴交点坐标为(-1,0)(1,0),
所以阴影部分的面积S=$\frac{1}{2}$×(1+1)×1=1,故本选项不符合题意;
D、函数y=x+2的图象和x轴的交点坐标为(2,0),和y轴的交点坐标为(0,2),
所以阴影部分的面积S=$\frac{1}{2}×2×2$=2,故本选项符合题意;
故选D.
点评 本题考查了抛物线与x轴的交点,坐标与图形性质、一次函数图象上点的坐标特征、反比例函数k的几何意义等知识点,能正确求出各个图象中阴影部分的面积是解此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 OB.
OB.
 等( )
等( ) B.
B.  C.
C.  D.
D. 
 的结果是( )
的结果是( ) B. 16
B. 16 C. 2a
C. 2a D. 2a
D. 2a
 B.
B.  C.
C.  D. 1
D. 1
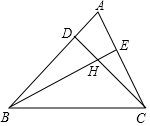 如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.