题目内容
【题目】综合与实践
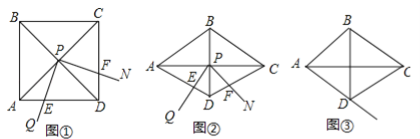
(1)问题发现

如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]() .请写出
.请写出![]() 的度数及线段
的度数及线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)类比探究
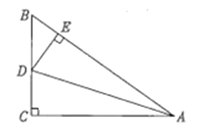
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.
填空:①![]() 的度数为____________;
的度数为____________;
②线段![]() 之间的数量关系为_______________________________.
之间的数量关系为_______________________________.
(3)拓展延伸
在(2)的条件下,若![]() ,则四边形
,则四边形![]() 的面积为______________.
的面积为______________.
【答案】(1)![]() ,证明详见解析;(2)①
,证明详见解析;(2)①![]() ;②
;②![]() ;(3)35
;(3)35
【解析】
(1)![]() 和
和![]() 均为等边三角形,根据等边三角形的性质即可证得
均为等边三角形,根据等边三角形的性质即可证得![]() ,所以
,所以![]() 即可求出
即可求出![]() ,证明出
,证明出![]() .
.
(2)①![]() 和
和![]() 均为等腰直角三角形,可证的
均为等腰直角三角形,可证的![]() ,因为
,因为![]() ,所以∠CED=∠CDE=45°,可得出
,所以∠CED=∠CDE=45°,可得出![]() ,②
,②![]() 为
为![]() 中
中![]() 边上的高,则DE=2CM,由全等可知EB=AD,即可得
边上的高,则DE=2CM,由全等可知EB=AD,即可得![]() .
.
(3) 四边形![]() 的面积等于△ACE的面积加上△AEB的面积,根据已知条件利用三角形的面积公式即可求解.
的面积等于△ACE的面积加上△AEB的面积,根据已知条件利用三角形的面积公式即可求解.
(1)结论:![]()
证明:![]() 和
和![]() 均为等边三角形
均为等边三角形
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,
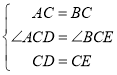
∴![]()
∴![]()
![]()
∴∠![]()
(2)解:∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
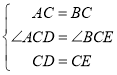
∴![]()
![]()
∵△DCE是等腰直角三角形
∴∠CDE=∠CED=45°
∴![]()
∴![]()
∵![]()
∴EB=AD
∵![]() 为
为![]() 中
中![]() 边上的高
边上的高
∴DE=2CM
∴![]()
(3)∵![]() ,
,![]()
∴AE=10
![]()

练习册系列答案
相关题目