题目内容
在四边形ABCD中,若AB⊥DC,且AD∥BC,则称四边形ABCD为平行四边形(即两组对边分别平行的四边形叫做平行四边形).
(1)已知:如图(1),四边形ABCD为平行四边形,求证:∠B=∠D;
(2)已知:如图(2),四边形EFGH中,EF∥HG,∠E=∠G,求证:四边形EFGH为平行四边形.
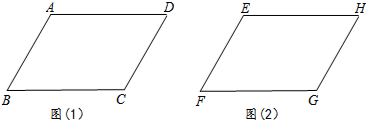
(1)已知:如图(1),四边形ABCD为平行四边形,求证:∠B=∠D;
(2)已知:如图(2),四边形EFGH中,EF∥HG,∠E=∠G,求证:四边形EFGH为平行四边形.
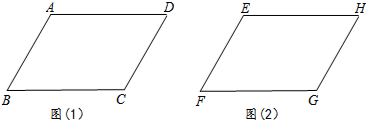
考点:平行线的判定与性质
专题:新定义
分析:(1)根据四边形ABCD为平行四边形,得出AB∥DC,AD∥BC,再根据平行线的性质得出∠A+∠D=180°,∠A+∠B=180,从而得出∠B=∠D;
(2)根据已知和平行线的性质得出∠E+∠H=180°,再根据∠E﹦∠G,得出∠G+∠H=180°,最后根据平行线的判定得出EH∥FG,从而得出四边形EFGH为平行四边形.
(2)根据已知和平行线的性质得出∠E+∠H=180°,再根据∠E﹦∠G,得出∠G+∠H=180°,最后根据平行线的判定得出EH∥FG,从而得出四边形EFGH为平行四边形.
解答:解:(1)∵四边形ABCD为平行四边形,
∴AB∥DC,AD∥BC,
∴∠A+∠D=180°,∠A+∠B=180°(两直线平行,同旁内角互补),
∴∠B﹦∠D(同角的补角相等);
(2)∵EF∥HG(已知),
∴∠E+∠H=180°(两直线平行,同旁内角互补),
∵∠E﹦∠G(已知),
∴∠G+∠H=180°(等量代换),
∴EH∥FG(同旁内角互补,两直线平行),
∴四边形EFGH为平行四边形(平行四边形定义).
∴AB∥DC,AD∥BC,
∴∠A+∠D=180°,∠A+∠B=180°(两直线平行,同旁内角互补),
∴∠B﹦∠D(同角的补角相等);
(2)∵EF∥HG(已知),
∴∠E+∠H=180°(两直线平行,同旁内角互补),
∵∠E﹦∠G(已知),
∴∠G+∠H=180°(等量代换),
∴EH∥FG(同旁内角互补,两直线平行),
∴四边形EFGH为平行四边形(平行四边形定义).
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目


 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=1.7m,斜面坡角为35°,求木箱端点E距地面AC的高度EF.(精确到0.1米)
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=1.7m,斜面坡角为35°,求木箱端点E距地面AC的高度EF.(精确到0.1米) 如图,在?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形.
如图,在?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形. 如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC、BC于点E、F,作GH∥BC分别交AB、AC于点G、H,作MN∥AC分别交AB、BC于点M、N.试求EF+GH+MN的值.
如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC、BC于点E、F,作GH∥BC分别交AB、AC于点G、H,作MN∥AC分别交AB、BC于点M、N.试求EF+GH+MN的值.