题目内容
15. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,-4),B(4,-4),C(1,-1).
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,-4),B(4,-4),C(1,-1).(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标(-2,-4);
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
分析 (1)根据题意画出即可;关于y轴对称点的坐标纵坐标不变,横坐标互为相反数;
(2)根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接即可;
(3)利用△ABC旋转时BC线段扫过的面积S扇形BOB2-S扇形COC2即可求出.
解答 (1)如图所示,A1坐标为(-2,-4),
故答案为:(-2,-4);
(2)如图所示.
(3)∵$OC=\sqrt{2}$,OB=$4\sqrt{2}$,
∴△ABC旋转时BC线段扫过的面积S扇形BOB2-S扇形COC2=$\frac{90°πO{B}^{2}}{360°}$-$\frac{90°π•O{C}^{2}}{360°}$=$\frac{90°π(32-2)}{360°}$=$\frac{15π}{2}$.
点评 本题考查了利用旋转变换作图,轴对称和扇形面积公式等知识,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.有一组数据:1,4,-3,3,4,这组数据的中位数为( )
| A. | -3 | B. | 1 | C. | 3 | D. | 4 |
20.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (-2ab)2=4a2b2 | C. | (a2)3=a5 | D. | 3a3b2÷a2b2=3ab |
4.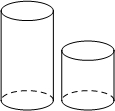 图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )
图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )
 图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )
图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )| A. | 主视图相同 | B. | 俯视图相同 | ||
| C. | 左视图相同 | D. | 主视图、俯视图、左视图都相同 |
 由几个相同的小正方形搭成的一个几何体如图所示,这个几何体的主视图是( )
由几个相同的小正方形搭成的一个几何体如图所示,这个几何体的主视图是( )


