题目内容
10．在Rt△ABC中，∠A=90°，AB=3，BC=4，则AC=（ ）| A． | 5 | B． | 4 | C． | $\sqrt{7}$ | D． | 5或$\sqrt{7}$ |
分析 根据勾股定理计算即可．
解答 解：在Rt△ABC中，∠A=90°，
由勾股定理得，AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{7}$，
故选：C．
点评 本题考查的是勾股定理的应用，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
相关题目
20．
如图，?ABCD的对角线AC、BD相交于点O，点E是CD的中点，△ABD的周长为8cm，则△DOE的周长是（ ）
如图，?ABCD的对角线AC、BD相交于点O，点E是CD的中点，△ABD的周长为8cm，则△DOE的周长是（ ）| A． | 8cm | B． | 6cm | C． | 4cm | D． | 2cm |
18．
如图，△ABC中，AB=AC=10，DE是AB的中垂线，△BCD的周长为16，则BC的长为（ ）
如图，△ABC中，AB=AC=10，DE是AB的中垂线，△BCD的周长为16，则BC的长为（ ）| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
2．某市“单独两孩”政策开始实施，该政策的实施可能给我们的生活带来一些变化，人口计生部门抽样调查了部分市民（每个参与调查的市民必须且只能在以下6种变化中选择一项），并将调查结果绘制成绕计图．
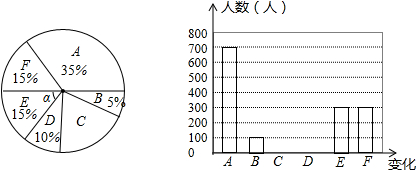
（1）参与调查的市民一共有2000人；
（2）参与调查的市民中选择C的人数是400人；
（3）∠α=54°；
（4）请补全条形统计图．
| 种类 | A | B | C | D | E | F |
| 变化 | 有利于延缓社会老龄化现象 | 导致人口暴增 | 提升家庭抗风险能力 | 增大社会基本公共服务压力 | 缓解男女比例不平衡的现象 | 促进人口与社会、资源、环境的协调可持续发展 |
（1）参与调查的市民一共有2000人；
（2）参与调查的市民中选择C的人数是400人；
（3）∠α=54°；
（4）请补全条形统计图．