��Ŀ����
������֣�
��ͼ1����O��Rt��ABC�����Բ����ABC=90�㣬��BD=BA��BE��DC��DC���ӳ����ڵ�E����֤��BE�ǡ�O�����ߣ�
���������
����OB��Ҫ֤��BE�ǡ�O�����ߣ�ֻҪ֤��OB ____ BE��������֪��E=90�㣬��ֻ��֤��OB ___ DE��
�ⷨ̽����
��1��С��������������������̽�����벹ȫ����֤��˼·��
��ͼ2������AD���ɡ�ECB��Բ�ڽ��ı���ABCD��һ����ǣ���֤��ECB=��BAD����ΪOB=OC������ __ ����ΪBD=BA������ ______ ������ͬ�����Ե�Բ�ܽ���Ⱥ͵����������õ� ____ ������DE��OB���Ӷ�֤����BE�ǡ�O�����ߣ�
��2����ͼ3������AD����ֱ��BF��AD�ڵ�H��С������BF��AD����˵�����ɣ�
��3������С���ķ��֣���֤��BE�ǡ�O�����ߣ���Ҫ��������ֲ�ͬ��֤����������

��ϰ��ϵ�д�
�����Ŀ



 =x�����������º���δ֪���ķ��̽����������̣�����ͨ����������ƽ������ת��Ϊ2x+3=x2�����x1=3��x2=��1������������ƽ�������ܲ���������������Ҫ���飬�����飬x2=��1��ԭ���̵���������ȥ������ԭ���̵Ľ���x=3��
=x�����������º���δ֪���ķ��̽����������̣�����ͨ����������ƽ������ת��Ϊ2x+3=x2�����x1=3��x2=��1������������ƽ�������ܲ���������������Ҫ���飬�����飬x2=��1��ԭ���̵���������ȥ������ԭ���̵Ľ���x=3��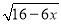 =x��
=x�� =6��
=6��
 ��BE=2����BC�ij���
��BE=2����BC�ij���
