Question

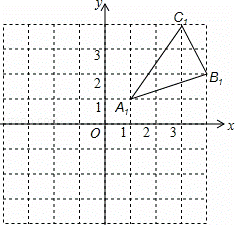
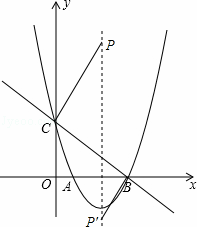
如图，在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A（1，0），C（0，3），且BC=5．

（1）分别求直线BC和抛物线的解析式（关系式）；

（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

      解：（1）∵C（0，3），即OC=3，BC=5，

∴在Rt△BOC中，根据勾股定理得：OB==4，即B（4，0），

把B与C坐标代入y=kx+n中，得：，

解得：k=﹣，n=3，

∴直线BC解析式为y=﹣x+3；

由A（1，0），B（4，0），设抛物线解析式为y=a（x﹣1）（x﹣4）=ax²﹣5ax+4a，

把C（0，3）代入得：a=，

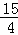则抛物线解析式为y=x²﹣x+3；

（2）存在．

如图所示，分两种情况考虑：

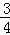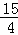∵抛物线解析式为y=x²﹣x+3，

∴其对称轴x=﹣=﹣=．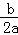

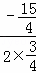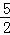当PC⊥CB时，△PBC为直角三角形，

∵直线BC的斜率为﹣，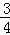

∴直线PC斜率为，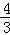

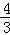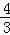∴直线PC解析式为y﹣3=x，即y=x+3，

与抛物线对称轴方程联立得，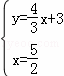

解得：，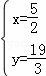

此时P（，）；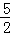

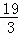当P′B⊥BC时，△BCP′为直角三角形，

同理得到直线P′B的斜率为，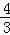

∴直线P′B方程为y=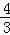（x﹣4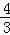）=x﹣，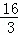

与抛物线对称轴方程联立得：，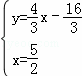

解得：，

此时P′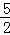（，﹣2）．

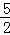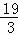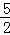综上所示，P（，）或P′（，﹣2）．