题目内容
20.已知函数y=x2-2x+2在t≤x≤t+1范围内的最小值为s,写出函数s关于t的函数解析式,并写出t的取值范围.分析 由题意可知,要求其在t≤x≤t+1范围内的最小值为s,主要是分三种情况(区间在对称轴的左边、右边、之间)讨论可得二次函数的最小值即得s的函数表达式.
解答 解:据题意可知函数为二次函数且开口向上,所以函数有最小值,即当x=-$\frac{-2}{2}$=1,ymin=1,
分情况讨论函数在闭区间在t≤x≤t+1范围内:
①当闭区间[t,t+1](t∈R)?(-∞,1)即t<0时,得:二次函数在x=t+1时取到最小值,
∴s=(t+1)2-2(t+1)+2=t2+1;
②当1∈[t,t+1]即0≤t≤1时,得x=1时,二次函数取到最小值,s=1;
③当闭区间[t,t+1]?(1,+∞)即t>1时,得:x=t时,二次函数取到最小值,s=t2-2t+2.
综上:s=$\left\{\begin{array}{l}{{t}^{2}+1(t<0)}\\{1(0≤t≤1)}\\{{t}^{2}-2t+2(t>1)}\end{array}\right.$.
点评 此题主要考查了二次函数的图象,解题时要根据区间与对称轴的位置进行分类讨论,主要是分三种情况(区间在对称轴的左边、右边、之间),解题时注意总结分类讨论思想在求解本题中的作用.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.在函数y=-$\frac{{a}^{2}+1}{x}$(a为常数)的图象上有点A(-1,y1),B($\frac{1}{4}$,y2),C($\frac{1}{2}$,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y3<y1 | D. | y2<y1<y3 |
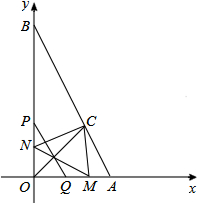 如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.
如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.