题目内容
 如图正方形ABCD在直角坐标系中关于y轴对称,若点A坐标为(1,0),则正方形ABCD的周长是
如图正方形ABCD在直角坐标系中关于y轴对称,若点A坐标为(1,0),则正方形ABCD的周长是考点:正方形的性质,坐标与图形性质
专题:
分析:因为四边形ABCD是正方形,所以AC=BD,AC和BD互相垂直平分,易知OB=1,根据勾股定理即可求得AB,根据正方形周长公式即可求得.
解答:解:∵四边形ABCD是正方形,
∴AC和BD互相垂直平分,且AC=BD,
∵A,C两点关于y轴对称,点A坐标为(1,0),
∴OA=1
∴OB=1,
∴AB=
,
∴正方形ABCD的周长是4
.
故答案为4
.
∴AC和BD互相垂直平分,且AC=BD,
∵A,C两点关于y轴对称,点A坐标为(1,0),
∴OA=1
∴OB=1,
∴AB=
| 2 |
∴正方形ABCD的周长是4
| 2 |
故答案为4
| 2 |
点评:本题考查了正方形的性质:正方形的对角线相等且互相垂直平分,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面去括号中错误的是( )
| A、a+(b-c)=a+b-c |
| B、a-(b+c-d)=a-b-c-d |
| C、m+2(p-q)=m+2p-2q |
| D、x-3(y+z)=x-3y-3z |
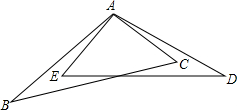 如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是
如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是