Question

【题目】如图，在每个小正方形边长为1的方格纸中，△的顶点都在方格纸格点上.将△向左平移2格，再向上平移4格．

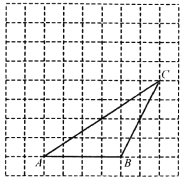
（1）请在图中画出平移后的△ ;

（2）图中AC和的关系 ；

（3）再在图中画出△的高;

（4）= ；

（5）在图中能使的格点的个数有 个(点异于C)．

Answer 1

【答案】（1）如图见解析；（2）平行且相等；（3）如图见解析；（4）8；（5）9．

【解析】

（1）利用网格特点和平移的性质，分别画出点A、B、C的对应点A′、B′、C′即可；

（2）由平移的性质，即可得这两条线段之间的关系；

（3）利用网格特点，作CD⊥AB于D；

（4）由三角形的面积的求解方法求解即可求得答案；

（5）利用同底等高模型，结合平行线的性质解决问题即可．

解：（1）如图①所示：

图①

（2）根据平移的性质可得：AC∥A′C′，AC=A′C′；
即这两条线段之间的关系是平行且相等．
故答案为：平行且相等．

（3）如图①所示：过点C作线段AB的垂线，交线段AB的延长线于点D.

（4）S△ABC=ABCD=×4×4=8；
故答案为：8；

（5）∵，AB=4，∴点P到直线AB的距离为4，结合图形，满足条件的格点P有9个，在经过点C与直线AB平行的直线上，如图②所示：

图①

故答案为：9