Question

【题目】如图，在平面直角坐标系中，点P（1，﹣4）、Q（m，n）在函数（x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（ ）

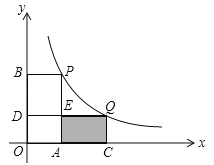
A．减小 B．增大 C．先减小后增大 D．先增大后减小

Answer 1

【答案】B．

【解析】

试题分析：AC=m﹣1，CQ=n，则S四边形ACQE=ACCQ=（m﹣1）n=mn﹣n．

∵Q（m，n）在函数（x＞0）的图象上，∴mn=k=﹣4（常数），∴S四边形ACQE=ACCQ=（m﹣1）n=﹣4﹣n，∵当m＞1时，n随m的增大而减小，∴S四边形ACQE=﹣4﹣n随m的增大而增大．故选B．