题目内容
18.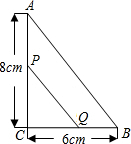 在Rt△ACB中,∠C=90°,点P、Q同时由A、B两点出发分别沿AC、BC方向向点C匀速移动,点P的速度是2m/s,点Q的速度是1m/s.其中一点到终点,另一点也随之停止移动.
在Rt△ACB中,∠C=90°,点P、Q同时由A、B两点出发分别沿AC、BC方向向点C匀速移动,点P的速度是2m/s,点Q的速度是1m/s.其中一点到终点,另一点也随之停止移动.(1)几秒后△PCQ为等腰三角形?
(2)几秒后四边形ABQP的面积为Rt△ACB面积的三分之一?
分析 (1)根据等腰三角形的两腰相等列出一元一次方程求解即可;
(2)分别表示出PC和QC的长,利用三角形的面积公式列出方程求解即可.
解答 解:(1)设x秒后,△PCQ是等腰三角形,
则PC=(8-2x)cm,QC=(6-x)cm,
∵△PCQ为等腰三角形,
∴PC=QC,
即:8-2x=6-x,
解得:x=2,
∴2秒后△PCQ为等腰三角形;
(2)设y秒后四边形ABQP的面积为Rt△ACB面积的三分之一,
根据题意得:$\frac{1}{2}$(8-2y)(6-y)=$\frac{1}{3}$×$\frac{1}{2}$×6×8,
解得:y=2或y=8(舍去).
答:2秒后四边形ABQP的面积为Rt△ACB面积的三分之一.
点评 本题考查了一元一次方程及一元二次方程的应用,解题的关键是能够表示出有关线段的长,难度不大.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6. 如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上.△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=4,则△A6B6A7的边长为( )
如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上.△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=4,则△A6B6A7的边长为( )
 如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上.△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=4,则△A6B6A7的边长为( )
如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上.△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=4,则△A6B6A7的边长为( )| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
3.把(-5)-(+7)+(-3)+(-11)写成省略加号的代数和的形式,正确的是( )
| A. | -5+7-3-11 | B. | (-5)(+7)(-3)(-11) | C. | -5-7-3-11 | D. | -5-7+-3+11 |
10.对于任意有理数a,下列结论正确的是( )
| A. | |a|是正数 | B. | -a是负数 | C. | -|a|是负数 | D. | -|a|不一定是负数 |
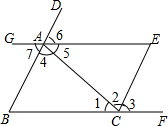 如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.
如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.