题目内容
如图MN∥AB，P、Q为直线MN上的任意两点，三角形PAB的面积为S1，三角形QAB的面积为S2，则
- A.S1＜S2
- B.S1=S2
- C.S1＞S2
- D.不能确定
B
分析：过P作PE⊥AB于E，过Q作QF⊥AB于F，得出四边形PEFQ是平行四边形，推出PE=PF，根据S△PAB=
×AB×PE，S△QAB=×AB×QF推出S1=S2即可．
解答：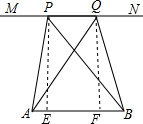
过P作PE⊥AB于E，过Q作QF⊥AB于F，
则PE∥QF，
∵MN∥AB，
∴四边形PEFQ是平行四边形，
∴PE=PF，
∴S△PAB=×AB×PE，S△QAB=×AB×QF，
∴S1=S2，
故选B．
点评：本题考查了三角形的面积和平行线间的距离的应用，注意：等底等高的三角形面积相等．
分析：过P作PE⊥AB于E，过Q作QF⊥AB于F，得出四边形PEFQ是平行四边形，推出PE=PF，根据S△PAB=
×AB×PE，S△QAB=×AB×QF推出S1=S2即可．解答：
过P作PE⊥AB于E，过Q作QF⊥AB于F，
则PE∥QF，
∵MN∥AB，
∴四边形PEFQ是平行四边形，
∴PE=PF，
∴S△PAB=
×AB×PE，S△QAB=×AB×QF，∴S1=S2，
故选B．
点评：本题考查了三角形的面积和平行线间的距离的应用，注意：等底等高的三角形面积相等．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
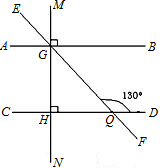19、如图MN⊥AB，MN⊥CD，垂足分别为G，H，直线EF交AB、CD于点G、Q，∠GQD=130°．
如图MN∥AB，P、Q为直线MN上的任意两点，三角形PAB的面积为S1，三角形QAB的面积为S2，则（ ）
如图MN⊥AB，MN⊥CD，垂足分别为G，H，直线EF交AB、CD于点G、Q，∠GQD=130°．求∠EGA与∠HGQ的度数．