题目内容
9.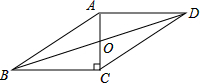 如图,在?ABCD中,AB=10,AD=8,AC⊥BC,下列计算错误的是( )
如图,在?ABCD中,AB=10,AD=8,AC⊥BC,下列计算错误的是( )| A. | BC=8 | B. | BD=15 | C. | AC=6 | D. | ?ABCD的面积是48 |
分析 利用平行四边形的性质结合勾股定理和平行四边形的面积求法分别分析得出即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=8,
∴选项A正确,不合题意;
∵AB=10,BC=8,AC⊥BC,
∴AC=6,故选项C正确,不合题意,
故?ABCD的面积是:6×8=48,
AC与BD相交于点O,
∴AO=CO=3,
∴BO=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$,
∴BD=2$\sqrt{73}$,
故选项B错误,符合题意;
故选:B.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,利用勾股定理得出AC的长是解题关键.

练习册系列答案
相关题目
1. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )| A. | 16cm | B. | 22cm | C. | 20cm | D. | 24cm |
18.下列长度的三条线段能组成三角形的是( )
| A. | 3、4、8 | B. | 5、6、11 | C. | 5、6、10 | D. | 3、8、12 |
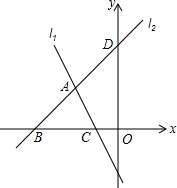 如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.
如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.
 如图在网格中按要求画出图形,先将△ABC向下平移5格得到△A1B1C1,再以点O为旋转中心将ABC沿顺时针旋转90°得到△A2B2C2.
如图在网格中按要求画出图形,先将△ABC向下平移5格得到△A1B1C1,再以点O为旋转中心将ABC沿顺时针旋转90°得到△A2B2C2.