题目内容
7.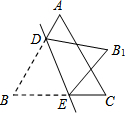 如图,点D,E分别在等边△ABC的边AB,BC上,将△BDE沿直线DE翻折,使点B落在B1处.若∠ADB1=70°,则∠CEB1=50°.
如图,点D,E分别在等边△ABC的边AB,BC上,将△BDE沿直线DE翻折,使点B落在B1处.若∠ADB1=70°,则∠CEB1=50°.
分析 由等边三角形的性质可知:∠B=60°,由邻补角的定义可知∠BDB1=110°,然后由翻折的性质可求得∠BDE=55°,△BDE中由三角形的内角和定理可求得∠BED=65°,然后由翻折的性质可知∠BEB1=130°,从而可求得∠CEB1=50°.
解答 解:由翻折的性质可知:∠BDE=∠B1DE,
∵∠ADB=70°,
∴∠BDE=$\frac{1}{2}$∠BDB1=$\frac{1}{2}×110°$=55°,
∵△ABC为等边三角形,
∴∠B=60°.
在△BDE中,∠BED=180°-55°-60°=65°.
由翻折的性质可知:∠BEB1=2×65°=130°
∴∠CEB1=180°-130°=50°.
故答案为:50°.
点评 本题主要考查的是翻折变换,利用翻折的性质找出图中相等的角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.-|-π|的相反数是( )
| A. | -兀 | B. | π | C. | 3.14 | D. | -3.14 |
2. 将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
 将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.计算(2x3)2的结果是( )
| A. | 4x6 | B. | 2x6 | C. | 4x5 | D. | 2x5 |
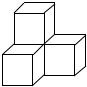 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
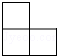


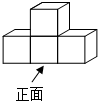 如图是由四个大小相同的正方体搭成的几何体,则它的主视图是( )
如图是由四个大小相同的正方体搭成的几何体,则它的主视图是( )