题目内容
已知,△ABC是等边三角形,点D为直线BC上一点(端点B、C除外),以AD为边作等边△ADF,连接CF.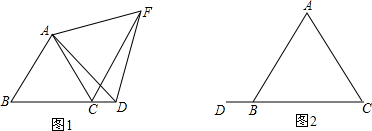
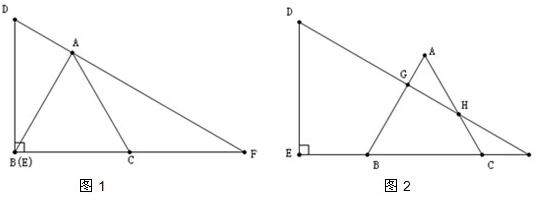
(1)如图1,点D在点C右边,①求证:BD=CF;②求∠FCD的度数;
(2)如图2,点D在点B左边,点F在直线BC下方,请先补全图形,并直接给出∠AFC与∠DAC之间满足的数量关系式为______.
(1)①证明:∵△ABC和△ADF都是等边三角形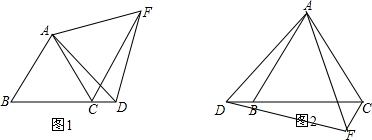 ,
,
∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAD=∠CAF,
在△ABD和△ACF中
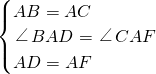 ,
,
∴△ABD≌△ACF,
∴BF=CF;
②解:∵△ABD≌△ACF,
∴∠ACF=∠ABD=60°,
又∵∠ACB=60°,
∴∠FCD=180°-(∠ACB+∠ACF)=60°;
(2)解:如图;
∵△ABC和△ADF都是等边三角,
∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC-∠BAF=∠DAF+∠BAF,
即∠BAD=∠CAF,
在△ABD和△ACF中
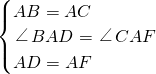 ,
,
∴△ABD≌△ACF,
∴∠ADB=∠AFC,∠DAB=∠FCA,
∴∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
故答案为∠AFC+∠DAC=120°.
分析:(1)①根据等边三角形的性质得AB=AC,AD=AF,∠BAC=∠DAF=60°,则∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,根据全等三角形的判定方法得到△ABD≌△ACF,
则BF=CF;②由△ABD≌△ACF得到∠ACF=∠ABD=60°,然后利用∠FCD=180°-(∠ACB+∠ACF)进行计算;
(2)根据题意画图,与①一样可证明△ABD≌△ACF,则∠ADB=∠AFC,∠DAB=∠FCA,于是∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.也考查了等边三角形的性质.
 ,
,∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAD=∠CAF,
在△ABD和△ACF中
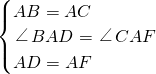 ,
,∴△ABD≌△ACF,
∴BF=CF;
②解:∵△ABD≌△ACF,
∴∠ACF=∠ABD=60°,
又∵∠ACB=60°,
∴∠FCD=180°-(∠ACB+∠ACF)=60°;
(2)解:如图;
∵△ABC和△ADF都是等边三角,
∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC-∠BAF=∠DAF+∠BAF,
即∠BAD=∠CAF,
在△ABD和△ACF中
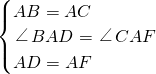 ,
,∴△ABD≌△ACF,
∴∠ADB=∠AFC,∠DAB=∠FCA,
∴∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
故答案为∠AFC+∠DAC=120°.
分析:(1)①根据等边三角形的性质得AB=AC,AD=AF,∠BAC=∠DAF=60°,则∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,根据全等三角形的判定方法得到△ABD≌△ACF,
则BF=CF;②由△ABD≌△ACF得到∠ACF=∠ABD=60°,然后利用∠FCD=180°-(∠ACB+∠ACF)进行计算;
(2)根据题意画图,与①一样可证明△ABD≌△ACF,则∠ADB=∠AFC,∠DAB=∠FCA,于是∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.也考查了等边三角形的性质.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
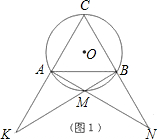

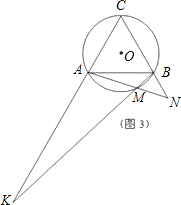
(1)如图1,图2,图3,M分别为
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
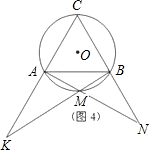
(2)如图4,当M为
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
已知,△ABC是等边三角形且内接于⊙O,取
 |
| AB |




(1)如图1,图2,图3,M分别为
 |
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 |
| AB |
(3)对(2)中提出的猜想,依图4给出证明.
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
