题目内容
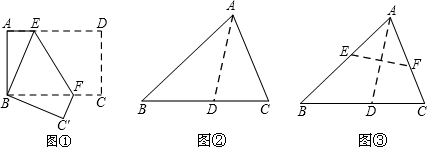
(1)操作:如图1,在线段AB所在的直线上取一点O(O点在线段外),将线段AB绕点O旋转一周,所得到的图形是个圆环(如图2),此圆环的面积就是线段AB所扫过的面积,已知AB=2,OA=1,则线段AB扫过的面积为
(2)如图3,在Rt△ABC中,∠C=90°,∠B=30°,AC=2,若将△ABC绕点A旋转一周,那么边BC扫过的图形为
(3)若将图3中的Rt△ABC绕点C旋转一周,则边AB扫过的图形是什么?面积为多少?
(结果中保留π)
分析:(1)线段AB所扫过的圆环的面积为大圆的面积减去小圆的面积,其中大圆半径OB=3,小圆半径OA=1,利用圆的面积公式计算即可;
(2)将△ABC绕点A旋转一周,那么边BC扫过的图形为圆环,它的面积为大圆的面积减去小圆的面积,其中大圆半径AB=4,小圆半径AC=2,利用圆的面积公式计算即可;
(3)Rt△ABC绕点C旋转一周,则边AB扫过的图形是圆环,它的面积为大圆的面积减去小圆的面积,其中小圆半径为C到AB的距离CE=
,大圆半径CB=2
,利用圆的面积公式计算即可;
(2)将△ABC绕点A旋转一周,那么边BC扫过的图形为圆环,它的面积为大圆的面积减去小圆的面积,其中大圆半径AB=4,小圆半径AC=2,利用圆的面积公式计算即可;
(3)Rt△ABC绕点C旋转一周,则边AB扫过的图形是圆环,它的面积为大圆的面积减去小圆的面积,其中小圆半径为C到AB的距离CE=
| 3 |
| 3 |
解答: 解:(1)∵AB=2,OA=1,
解:(1)∵AB=2,OA=1,
∴OB=3,
∴S圆环=π(OB2-OA2)=π(9-1)=8π;
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,AC=2,
∴AB=2AC=4,
∵将△ABC绕点A旋转一周,那么边BC扫过的图形为圆环,
∴边BC扫过的图形面积=π(AB2-AC2)=π(42-22)=12π;
(3)过C作CE⊥AB,如图,
Rt△ABC绕点C旋转一周,则边AB扫过的图形是以CE和CB为半径的两圆形成的圆环,
∵∠B=30°,AC=2,
∴BC=2
,
∴CE=
,
∴S圆环=π(CB2-CE2)=π(12-3)=9π.
故答案为8π;圆环,12π.
 解:(1)∵AB=2,OA=1,
解:(1)∵AB=2,OA=1,∴OB=3,
∴S圆环=π(OB2-OA2)=π(9-1)=8π;
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,AC=2,
∴AB=2AC=4,
∵将△ABC绕点A旋转一周,那么边BC扫过的图形为圆环,
∴边BC扫过的图形面积=π(AB2-AC2)=π(42-22)=12π;
(3)过C作CE⊥AB,如图,
Rt△ABC绕点C旋转一周,则边AB扫过的图形是以CE和CB为半径的两圆形成的圆环,
∵∠B=30°,AC=2,
∴BC=2
| 3 |
∴CE=
| 3 |
∴S圆环=π(CB2-CE2)=π(12-3)=9π.
故答案为8π;圆环,12π.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了含30的直角三角形三边的关系以及圆的面积公式.

练习册系列答案
相关题目



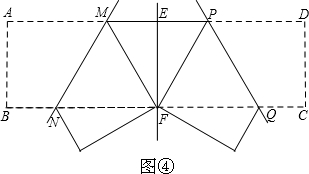
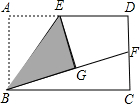 (2011•曲阜市模拟)(1)操作发现
(2011•曲阜市模拟)(1)操作发现