题目内容
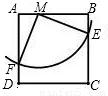
（2011•曲阜市模拟）（1）操作发现如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
（2）问题解决
保持（1）中的条件不变，DC=2DF，求
| AD | AB |
分析：（1）连接EF，则AE=EG，可证明Rt△EGF≌Rt△EDF，则GF=DF，∠GEF=∠DEF，∠GFE=∠DFE，∠AEB=∠GEB，从而得出△EDF∽△BAE∽△BEF；
（2）设DF=x，BC=y，则有GF=x，AD=y．根据DC=2DF得到CF=x，DC=AB=BG=2x，BF=BG+GF=3x，然后利用勾股定理得到y与x之间关系，从而求得两条线段的比．
（2）设DF=x，BC=y，则有GF=x，AD=y．根据DC=2DF得到CF=x，DC=AB=BG=2x，BF=BG+GF=3x，然后利用勾股定理得到y与x之间关系，从而求得两条线段的比．
解答：
解：（1）同意．连接EF，则∠EGF=∠D=90°，
在Rt△EGF和Rt△EDF中
∴Rt△EGF≌Rt△EDF（HL）．
∴GF=DF；
（2）由（1）知，GF=DF．设DF=x，BC=y，则有GF=x，AD=y．
∵DC=2DF，
∴CF=x，DC=AB=BG=2x，
∴BF=BG+GF=3x．
在Rt△BCF中，由勾股定理得：BC2+GF2=BF2，即y2+x2=（3x）2．
∴y=2
x
∴
=
=
；
解：（1）同意．连接EF，则∠EGF=∠D=90°，在Rt△EGF和Rt△EDF中
|
∴Rt△EGF≌Rt△EDF（HL）．
∴GF=DF；
（2）由（1）知，GF=DF．设DF=x，BC=y，则有GF=x，AD=y．
∵DC=2DF，
∴CF=x，DC=AB=BG=2x，
∴BF=BG+GF=3x．
在Rt△BCF中，由勾股定理得：BC2+GF2=BF2，即y2+x2=（3x）2．
∴y=2
| 2 |
∴
| AD |
| AB |
| y |
| 2x |
| 2 |
点评：本题考查了相似三角形的判定和性质、全等三角形的判定和性质以及翻折的性质，难度较大．
练习册系列答案
相关题目
（2011•曲阜市模拟）如图，在方格纸上建立的平面直角坐标系中，将Rt△ABC绕点C按顺时针方向旋转90°，得到Rt△FEC，则点A的对应点F的坐标是
