题目内容
【题目】如图，在矩形
中，
，
，
为
边上一点，将
沿
翻折，点
落在点
处，当
为直角三角形时，
________.
【答案】3或6
【解析】
对直角
中那个角是直角分三种情况讨论，再由折叠的性质和勾股定理可BE的长.
解：如图，若∠AEF=90°
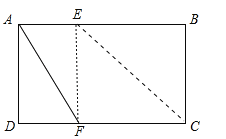
∵∠B=∠BCD=90°=∠AEF
∴四边形BCFE是矩形
∵将ABEC沿着CE翻折
∴CB=CF
∵四边形BCFE是正方形
∴BE=BC-AD=6，
如图，若∠AFE=90°
∵将△BEC沿着CE翻折
∴CB=CF=6，∠B=∠EFC=90°，BE=EF
∵∠AFE+∠EFC=180°
∴点A，点F，点C三点共线
∴
∴AF=AC-CF=4
∵
∴
∴BE=3，
若∠EAF=90°，
∵CD=8> CF=6
∴点F不可能落在直线AD上
∴.不存在∠EAF=90
综上所述：BE=3或6
故答案为：3或6
练习册系列答案
相关题目
