Question

【题目】如图，二次函数的图象与轴交于两点，，其中．下列四个结论：①；②；③；④，正确的个数是( )

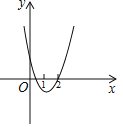
A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

根据抛物线的开口方向、对称轴的位置、与y轴的交点可依次确定a、b、c的符号，进而可判断①；

根据对称轴的位置可得a、b的关系，再根据当时，，把得出的a、b的关系式代入整理即可判断②；

除以4可得，即为当时的值，再结合图象判断和x1的关系即可判断③；

易判断，展开整理再结合即可判断④．

解：①∵抛物线开口向上，∴，

∵抛物线对称轴在轴的右侧，∴，

∵抛物线与轴的交点在轴上方，∴，

∴，所以①正确；

②∵图象与轴交于两点，，其中，

∴，∴，

当时，，

∵当时，，

∴，∴，∴，故②正确；

③当时，值为，给乘以4，即可化为，

∵当时，由图象可知在和x1之间为正值，当时，在和x1之间为负值，∴与0的关系不能确定，故③错误；

④∵，∴，∴，

即，∴，

∵，，∴，

∴，即.

所以④正确．

综上，正确的是①②④，共3个，故选：C．