题目内容
2.如图①,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD.(1)图①中有2对全等三角形,并把它们写出来△ABF≌△CDE,△GBF≌△GDE;
(2)求证:BG=DG,AG=CG;
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
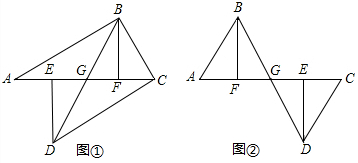
分析 (1)根据AE=CF,得到AF=CE,根据直角三角形的判定定理证明Rt△ABF≌Rt△CDE,根据AAS证明△GBF≌△GDE;
(2)根据全等三角形的性质定理证明即可;
(3)与(1)的证明方法相似,根据全等三角形的判定定理和性质定理证明.
解答 解:(1)∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$,
∴Rt△ABF≌Rt△CDE,
∵DE⊥AC,BF⊥AC,
∴∠DEG=∠BFG=90°,又∠DGE=∠BGF,DE=BF,
∴△GBF≌△GDE,
故答案为:2;△ABF≌△CDE,△GBF≌△GDE;
(2)∵△GBF≌△GDE,
∴BG=DG,EG=GF,
∵AE=CF,
∴AG=CG;
(3)在Rt△ABF和Rt△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$,
∴Rt△ABF≌Rt△CDE,
∴BG=DG,
在△BFG和△DEG中,
$\left\{\begin{array}{l}{∠BFG=∠DEG}\\{∠BGF=∠DGE}\\{BF=DE}\end{array}\right.$,
∴△BFG≌△DEG,
∴FG=EG,
则FG+AF=EG+CE,即AG=CG.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
11.已知$\frac{x+5}{16}$是一个最简真分数,那么x可以取的自然数有( )个.
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
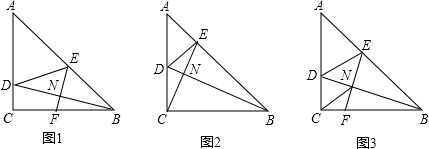
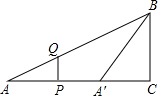 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.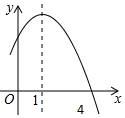 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.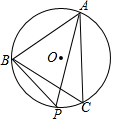 如图,△ABC内接于圆O,∠P=60°,弧$\widehat{BC}$=弧$\widehat{CA}$,则△ABC的特殊形状是等边三角形.
如图,△ABC内接于圆O,∠P=60°,弧$\widehat{BC}$=弧$\widehat{CA}$,则△ABC的特殊形状是等边三角形.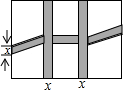 如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x m,根据条件,可列出方程:x2-35x+34=0.
如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x m,根据条件,可列出方程:x2-35x+34=0.