Question

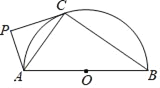
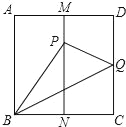
【题目】如图，正方形ABCD中，AB=1，M，N分别是AD，BC边的中点，沿BQ将△BCQ折叠，若点C恰好落在MN上的点P处，则PQ的长为（　　）

A. B. C. D.

Answer 1

【答案】B

【解析】

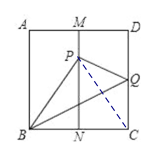
如下图，连接PC，由已知条件易得MN是BC的垂直平分线，由此可得PB=PC，由折叠的性质可得PB=CB，∠CBQ=∠PBQ=∠PBC，从而可得△PBC是等边三角形，即可得到∠CBQ=30°，结合∠BCQ=90°，设PQ=CQ=x，则可得BQ=2x，由此在Rt△CBQ中由勾股定理建立方程即可求得PQ的长.

如下图，就PC，

∵四边形ABCD是正方形，点M、N分别是AD和BC的中点，

∴可得MN是BC的垂直平分线，

∴PB=PC，

由折叠的性质可得：PB=CB，∠CBQ=∠PBQ=∠PBC，PQ=CQ，

∴PB=PC=BC，

∴△PBC是等边三角形，

∴∠PBC=60°，

∴∠CBQ=30°，

又∵在正方形ABCD中，∠BCQ=90°，

∴BQ=2CQ，

设CQ=x，则BQ=2x，

∵在Rt△CBQ中，BQ2=BC2+CQ2，

∴，解得：，

∴PQ=CQ=.

故选B.