题目内容
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
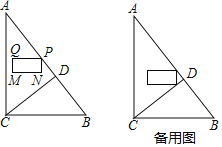
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
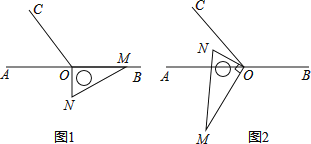
(1)将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿顺时针方向旋转,使
的速度沿顺时针方向旋转,使![]() 落在
落在![]() 上.在旋转的过程中,假如第
上.在旋转的过程中,假如第![]() 秒时,
秒时,![]() 、
、![]() 、
、![]() 三条射线构成的角中有两个角相等,求此时
三条射线构成的角中有两个角相等,求此时![]() 的值为多少?
的值为多少?
(2)将图1中的三角板绕点![]() 顺时针旋转(如图2),使
顺时针旋转(如图2),使![]() 在
在![]() 的内部,请探究:
的内部,请探究:![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)t=3或t=12;(2)∠AOM-∠NOC=30,理由见解析
【解析】
(1)根据已知条件可知,在第t秒时,三角板转过的角度为10°t,然后按照OA、OC、ON三条射线构成相等的角分两种情况讨论,即可求出t的值;
(2)根据三角板∠MON=90°可求出∠AOM、∠NOC和∠AON的关系,然后两角相加即可求出二者之间的数量关系.
解:(1)由题意得,![]()
①当![]()
![]()
此时,ON旋转了![]()
![]()

②当![]() 此时
此时![]()
![]()
此时,ON旋转了![]()
![]()

综上所述,![]()
(2)![]()
理由如下:![]()
![]()
![]()
![]()
![]()

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目