题目内容
2.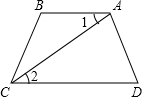 如图,已知∠B=140°,CA平分∠BCD,AB∥CD,求∠1的大小.
如图,已知∠B=140°,CA平分∠BCD,AB∥CD,求∠1的大小.
分析 首先根据平行线的性质,求出∠BCD,∠1=∠2,然后利用角平分线的定义求出∠2即可.
解答 解:∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=140°,
∴∠BCD=40°;
又∵CA平分∠BCD,
∴∠2=20°,
∵AB∥CD,
∴∠1=∠2=20°.
点评 本题考查了平行线的性质及角平分线的定义,熟练掌握性质定理是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
13.一次函数的图象经过点(2,1)和(-1,-3),则它的解析式为( )
| A. | $y=\frac{3}{4}x-\frac{5}{3}$ | B. | $y=\frac{4}{3}x-\frac{3}{5}$ | C. | $y=\frac{3}{4}x+\frac{3}{5}$ | D. | $y=\frac{4}{3}x-\frac{5}{3}$ |
17.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元; 乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
按上述优惠条件,若贝贝第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品各多少件?
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
11.顺次连结对角线垂直的四边形各边中点,所得四边形是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 任意四边形 |
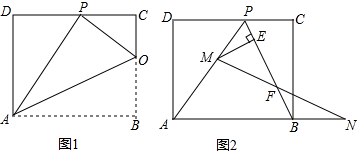
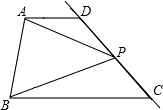 如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).
如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).