题目内容
△ABC的三边长分别是2、3、4,则另一个与它相似的三角形的最长边为10,则此三角形的周长为________,两个三角形的面积比为________.
22.5 4:25
分析:先求出△ABC的周长,再根据相似三角形的周长的比等于相似比列式求解即可;
根据相似三角形面积的比等于相似比的平方进行计算即可求解.
解答:△ABC的周长为:2+3+4=9,
是另一与它相似的三角形的周长为x,
则 =
=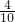 ,
,
解得x=22.5;
∵两三角形的相似比为4:10,即2:5,
∴两个三角形的面积比为:(2:5)2=4:25.
故答案为:22.5,4:25.
点评:本题主要考查了相似三角形周长的比等于相似比,面积的比等于相似比的平方的性质,熟记性质是解题的关键.
分析:先求出△ABC的周长,再根据相似三角形的周长的比等于相似比列式求解即可;
根据相似三角形面积的比等于相似比的平方进行计算即可求解.
解答:△ABC的周长为:2+3+4=9,
是另一与它相似的三角形的周长为x,
则
 =
=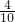 ,
,解得x=22.5;
∵两三角形的相似比为4:10,即2:5,
∴两个三角形的面积比为:(2:5)2=4:25.
故答案为:22.5,4:25.
点评:本题主要考查了相似三角形周长的比等于相似比,面积的比等于相似比的平方的性质,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC的三边长分别为:6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
| A、2cm,3cm | B、4cm,5cm | C、5cm,6cm | D、6cm,7cm |