题目内容
7.如本题图①,在△ABC中,已知∠ABC=∠ACB=α.过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.(1)求∠ACD的大小;
(2)在线段CD的延长线上取一点F,以FD为角的一边作∠DFE=α,另一边交BD延长线于点E,若FD-kAD(如本题图②所示),试求$\frac{{S}_{△DEF}}{{S}_{△BCD}}$的值(用含k的代数式表示).
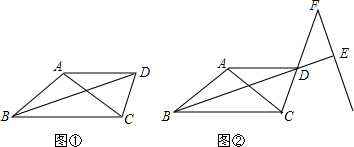
分析 (1)由∠ABC=∠ACB,BD平分∠ABC,得到∠1=∠2=$\frac{α}{2}$,AB=AC,因为AD∥BC,推出∠2=∠3,得到∠3=∠1=$\frac{α}{2}$,得到AB=AD.AC=AD=AB.于是得到∠ACD=∠ADC=$\frac{180°-∠CAD}{2}$,根据AD∥BC,∠CAD=ACB=α,得出结论∠ACD=∠ADC=$\frac{180°-α}{2}$=90°-$\frac{α}{2}$.
(2)过A作AH⊥BC于点H,得到∠AHB=90°.证出∠BAH=90°-α,因为AD∥BC,得出∠BDC+∠ADC=180°,然后证得对应角相等,得到相似三角形,根据相似三角形的性质得比例式求得结果.
解答 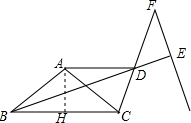 解:(1)∵∠ABC=∠ACB,BD平分∠ABC,
解:(1)∵∠ABC=∠ACB,BD平分∠ABC,
∴∠1=∠2=$\frac{α}{2}$,AB=AC,
∵AD∥BC,
∴∠2=∠3,
∴∠3=∠1=$\frac{α}{2}$,
∴AB=AD.
∴AC=AD=AB.
∴∠ACD=∠ADC=$\frac{180°-∠CAD}{2}$,
又∵AD∥BC,
∴∠CAD=ACB=α,
∴∠ACD=∠ADC=$\frac{180°-α}{2}$=90°-$\frac{α}{2}$.
(2)证明:过A作AH⊥BC于点H,
则∠AHB=90°.
∴∠BAH=90°-α,
∵AD∥BC,∴∠BCD+∠ADC=180°,
即:∠BCA+∠ACD+∠CDB+∠3=180°,
由∠ACB=α,∠ACD=90°-$\frac{α}{2}$,∠3=$\frac{α}{2}$,
得:∠CDB=180°-α-(90°-$\frac{α}{2}$)-$\frac{α}{2}$=90°-α.
∴∠FDE=∠CDB=90°-α,
∴∠BAH=∠FDE,∵∠ABH=∠DFE=α,
∴△ABH∽△DEF,
∵FD=kAD,AB=AD,
∴S△DEF=k2S△BAH,
∵AD∥BC,
∴S△BCD=S△ABC=2S△BAH,
∴$\frac{{S}_{△DEF}}{{S}_{△BCD}}$=$\frac{1}{2}$k2,
点评 本题考查了角平分线的性质,平行线的判定和性质,相似三角形的判定和性质,作辅助线构造相似三角形是解题的关键.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 10 | B. | 9 | C. | 8 | D. | 6 |
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )| A. | $\frac{\sqrt{3}}{2};\frac{\sqrt{3}}{n}$ | B. | $\frac{\sqrt{3}}{n};\frac{\sqrt{3}}{n}$ | C. | $\frac{\sqrt{3}}{2};\sqrt{3}$ | D. | $\sqrt{3}$;$\frac{\sqrt{3}}{n}$ |
 如图,AB∥CD,EF分别交AB、CD于E、F,∠1=55°,则∠2的度数是( )
如图,AB∥CD,EF分别交AB、CD于E、F,∠1=55°,则∠2的度数是( )| A. | 55° | B. | 125° | C. | 135° | D. | 145° |
| A. | 当AB=BC时,四边形ABCD是菱形 | B. | 当AC=BD时,四边形是正方形 | ||
| C. | 当∠ABC=90°时,四边形是矩形 | D. | 当AC⊥BD时,四边形是菱形 |
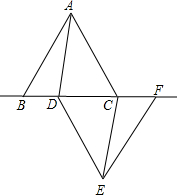 如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.
如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.