题目内容
在等腰三角形ABC中,AB=AC,腰AB的高CD与腰AC的夹角为30°,且CD= ,则底边BC的长为________.
,则底边BC的长为________.
4或
分析:分类讨论:当等腰三角形ABC为锐角三角形,由CD⊥AB,∠ACD=30°,得∠A=60°,根据含30度的直角三角形三边的关系得到DC= AD,AC=2AD,则易得AC=4,根据等腰三角形的性质由∠A=60°得△ABC为等边三角形,即可得到BC=4;当等腰三角形ABC为钝角三角形,由CD⊥AB,∠ACD=30°,得∠DAC=60°,而AB=AC,则∠B=30°,在Rt△BCD中根据含30度的直角三角形三边的关系即可得到BC的长.
AD,AC=2AD,则易得AC=4,根据等腰三角形的性质由∠A=60°得△ABC为等边三角形,即可得到BC=4;当等腰三角形ABC为钝角三角形,由CD⊥AB,∠ACD=30°,得∠DAC=60°,而AB=AC,则∠B=30°,在Rt△BCD中根据含30度的直角三角形三边的关系即可得到BC的长.
解答: 解:当等腰三角形ABC为锐角三角形,如图1,
解:当等腰三角形ABC为锐角三角形,如图1,
∵CD⊥AB,∠ACD=30°,
∴∠A=60°,
∴DC= AD,AC=2AD,
AD,AC=2AD,
而CD= ,
,
∴AD=2,
∴AC=4,
又∵AB=AC,而∠A=60°,
∴△ABC为等边三角形,
∴BC=4;
当等腰三角形ABC为钝角三角形,如图2,
∵CD⊥AB,∠ACD=30°,
∴∠DAC=60°,
∵AC=AB,
∴∠B=30°,
在Rt△BCD中,∠B=30°,CD-2 ,
,
∴BC=2CD=4 .
.
∴BC为4或4 .
.
故答案为:4或4 .
.
点评:本题考查了等腰三角形的性质:等腰三角形的两腰相等.也考查了含30度的直角三角形三边的关系以及分类讨论思想的运用.

分析:分类讨论:当等腰三角形ABC为锐角三角形,由CD⊥AB,∠ACD=30°,得∠A=60°,根据含30度的直角三角形三边的关系得到DC=
 AD,AC=2AD,则易得AC=4,根据等腰三角形的性质由∠A=60°得△ABC为等边三角形,即可得到BC=4;当等腰三角形ABC为钝角三角形,由CD⊥AB,∠ACD=30°,得∠DAC=60°,而AB=AC,则∠B=30°,在Rt△BCD中根据含30度的直角三角形三边的关系即可得到BC的长.
AD,AC=2AD,则易得AC=4,根据等腰三角形的性质由∠A=60°得△ABC为等边三角形,即可得到BC=4;当等腰三角形ABC为钝角三角形,由CD⊥AB,∠ACD=30°,得∠DAC=60°,而AB=AC,则∠B=30°,在Rt△BCD中根据含30度的直角三角形三边的关系即可得到BC的长.解答:
 解:当等腰三角形ABC为锐角三角形,如图1,
解:当等腰三角形ABC为锐角三角形,如图1,∵CD⊥AB,∠ACD=30°,
∴∠A=60°,
∴DC=
 AD,AC=2AD,
AD,AC=2AD,而CD=
 ,
,∴AD=2,
∴AC=4,
又∵AB=AC,而∠A=60°,
∴△ABC为等边三角形,
∴BC=4;
当等腰三角形ABC为钝角三角形,如图2,
∵CD⊥AB,∠ACD=30°,
∴∠DAC=60°,
∵AC=AB,
∴∠B=30°,
在Rt△BCD中,∠B=30°,CD-2
 ,
,∴BC=2CD=4
 .
.∴BC为4或4
 .
.故答案为:4或4
 .
.点评:本题考查了等腰三角形的性质:等腰三角形的两腰相等.也考查了含30度的直角三角形三边的关系以及分类讨论思想的运用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=
如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=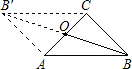 在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距
在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距 如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.
如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积. 如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是
如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是