题目内容
 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=15.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,求此时AM+NB的长.
如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=15.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,求此时AM+NB的长.考点:轴对称-最短路线问题
专题:
分析:MN表示直线a与直线b之间的距离,是定值,只要满足AM+NB的值最小即可,作点A关于直线a的对称点A′,并延长AA′,过点B作BE⊥AA′于点E,连接A′B交直线b于点N,过点N作NM⊥直线a,连接AM,则可判断四边形AA′NM是平行四边形,得出AM=A′N,由两点之间线段最短,可得此时AM+NB的值最小.过点B作BE⊥AA′,交AA′于点E,在Rt△ABE中求出BE,在Rt△A′BE中求出A′B即可得出AM+NB.
解答: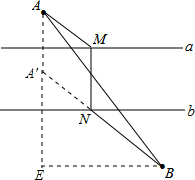 解:作点A关于直线a的对称点A′,并延长AA′,过点B作BE⊥AA′于点E,连接A′B交直线b于点N,过点N作NM⊥直线a,连接AM,
解:作点A关于直线a的对称点A′,并延长AA′,过点B作BE⊥AA′于点E,连接A′B交直线b于点N,过点N作NM⊥直线a,连接AM,
∵A到直线a的距离为2,a与b之间的距离为4,
∴AA′=MN=4,
∴四边形AA′NM是平行四边形,
∴AM+NB=A′N+NB=A′B,
过点B作BE⊥AA′,交AA′于点E,
易得AE=2+4+3=9,AB=15,A′E=2+3=5,
在Rt△AEB中,BE=
=12,
在Rt△A′EB中,A′B=
=13.
故AM+NB=13.
 解:作点A关于直线a的对称点A′,并延长AA′,过点B作BE⊥AA′于点E,连接A′B交直线b于点N,过点N作NM⊥直线a,连接AM,
解:作点A关于直线a的对称点A′,并延长AA′,过点B作BE⊥AA′于点E,连接A′B交直线b于点N,过点N作NM⊥直线a,连接AM,∵A到直线a的距离为2,a与b之间的距离为4,
∴AA′=MN=4,
∴四边形AA′NM是平行四边形,
∴AM+NB=A′N+NB=A′B,
过点B作BE⊥AA′,交AA′于点E,
易得AE=2+4+3=9,AB=15,A′E=2+3=5,
在Rt△AEB中,BE=
| AB2-AE2 |
在Rt△A′EB中,A′B=
| A′E2+BE2 |
故AM+NB=13.
点评:本题考查了勾股定理的应用、平行线之间的距离,解答本题的关键是找到点M、点N的位置,难度较大,注意掌握两点之间线段最短.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
在2,-2,0,-
四个数中,最小的数是( )
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、-
|
 在?ABCD中,E是边BC上的点,AE交对角线BD于点F,
在?ABCD中,E是边BC上的点,AE交对角线BD于点F, 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,AB=9,D为AB上一点,AD=3,连接CD,以CD为边等腰Rt△ECD,使∠ECD=90°,EC=CD,连接AE.
如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,AB=9,D为AB上一点,AD=3,连接CD,以CD为边等腰Rt△ECD,使∠ECD=90°,EC=CD,连接AE. 如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠α=
如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠α= 如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你动用所学知识找到破译的“钥匙”,目前,已破译出“今天考试”的真实意思是“努力发挥”,若“今”所处的位置为(x,y),则可发现“努”坐标与其有一定关系,根据其关系,破译“正做数学”的真实意思是( )
如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你动用所学知识找到破译的“钥匙”,目前,已破译出“今天考试”的真实意思是“努力发挥”,若“今”所处的位置为(x,y),则可发现“努”坐标与其有一定关系,根据其关系,破译“正做数学”的真实意思是( )