��Ŀ����
����Ŀ����֪��AOB=100��
��1����ͼ1��OCƽ�֡�AOB��OD��OE�ֱ�ƽ�֡�BOC�͡�AOC�����DOE�Ķ�����
��2����OCΪ��AOB����һ������ʱ����ͼ2��OD��OE���ǡ�BOC�͡�AOC��ƽ���ߣ���ʱ�ܷ������DOE�Ķ���������ܣ����������DOE�Ķ�����
��3����OCΪ��AOB����һ������ʱ����ͼ3��OD��OE���ǡ�BOC�͡�AOC��ƽ���ߣ���ʱ�ܷ������DOE�Ķ���������ܣ����������DOE�Ķ�����
��4��ͨ�����漸������̽��������һ����������ʾ.
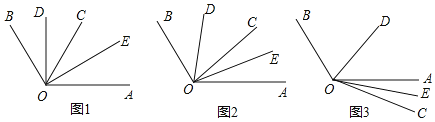
���𰸡���1����DOE=50�㣻��2����DOE=50�㣻��3����DOE=��50�㣻��4������OC�ڡ�AOB���ڲ������ⲿ,���С�DOE=50��.
��������
��1�����ݽ�ƽ���߶��������BOC�͡�AOC���������ɵó��𰸣�
��2�����ݽ�ƽ���߶���ó���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE�������DOE=��COD+��COE=
��AOE�������DOE=��COD+��COE=![]() ��AOB������������ɣ�
��AOB������������ɣ�
��3�����ݽ�ƽ���߶���ó���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE�������DOE=��COD-��COE=
��AOE�������DOE=��COD-��COE=![]() ��AOB������������ɣ�
��AOB������������ɣ�
��4���ɣ�1����2����3���ɵý���.
��1���ߡ�AOB=100�㣬0C�ǡ�AOB��ƽ���ߣ�
���AOB=��BOC=![]() ��AOB=50�㣬
��AOB=50�㣬
��OD��OE�ֱ�ƽ�֡�BOC����AOC��
���COD=![]() ��BOC=25�㣬��COE=
��BOC=25�㣬��COE=![]() ��AOC=25�㣬
��AOC=25�㣬
���DOE=��COD+��COE=25��+25��=50�㣻
��2����OD��OE�ֱ�ƽ�֡�BOC����AOC��
���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE��
��AOE��
���DOE=��COD+��COE=![]() ����BOE+��AOE��=
����BOE+��AOE��=![]() ��AOB=
��AOB=![]() ��100��=50�㣻
��100��=50�㣻
��3���ܣ�
��DOE=��DOC-��COE=![]() ��BOC-
��BOC-![]() ��AOC=
��AOC=![]() ����BOC-��AOC��=
����BOC-��AOC��=![]() ��AOB=
��AOB=![]() ��100��=50�㣮
��100��=50�㣮
��4���ɢ٢ڢۿ�֪:����OC�ڡ�AOB���ڲ������ⲿ,���С�DOE=![]() ��AOB=50��
��AOB=50��