题目内容
在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交BC于点E，过点A作直线CD的垂线交CD于点F，若AB=4，BC=6，则CE+CF的值为________．
10+
或2+
分析：根据平行四边形面积求出AE和AF，然后根据题意画出图形：有两种情况，求出BE、DF的值，求出CE和CF的值，继而求得出答案．
解答：∵四边形ABCD是平行四边形，
∴AB=CD=4，BC=AD=6，
①如图：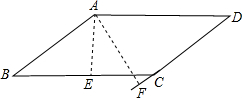
∵S?ABCD=BC•AE=CD•AF=12，
∴AE=2，AF=3，
在Rt△ABE中：BE=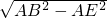
=2，
在Rt△ADF中，DF=
=3，
∴CE+CF=BC-BE+DF-CD=2+；
②如图：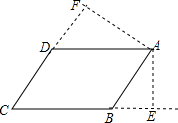
∵S?ABCD=BC•AE=CD•AF=12，
∴AE=2，AF=3，
在Rt△ABE中：BE=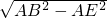=2，
在Rt△ADF中，DF==3，
∴CE+CF=BC+BE+DF+CD=10+；
综上可得：CE+CF的值为10+或2+．
故答案为：10+或2+．
点评：此题考查了平行四边形的性质以及勾股定理．此题难度适中，注意掌握分类讨论思想思想与数形结合思想的应用．
或2+分析：根据平行四边形面积求出AE和AF，然后根据题意画出图形：有两种情况，求出BE、DF的值，求出CE和CF的值，继而求得出答案．
解答：∵四边形ABCD是平行四边形，
∴AB=CD=4，BC=AD=6，
①如图：
∵S?ABCD=BC•AE=CD•AF=12，
∴AE=2，AF=3，
在Rt△ABE中：BE=
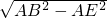=2，在Rt△ADF中，DF=
=3，∴CE+CF=BC-BE+DF-CD=2+
；②如图：
∵S?ABCD=BC•AE=CD•AF=12，
∴AE=2，AF=3，
在Rt△ABE中：BE=
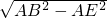=2，在Rt△ADF中，DF=
=3，∴CE+CF=BC+BE+DF+CD=10+
；综上可得：CE+CF的值为10+
或2+．故答案为：10+
或2+．点评：此题考查了平行四边形的性质以及勾股定理．此题难度适中，注意掌握分类讨论思想思想与数形结合思想的应用．
练习册系列答案
相关题目
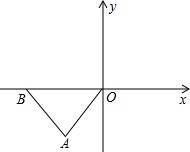如图，在下面直角坐标系中，已知A（-4，a），B（-8，0）