题目内容
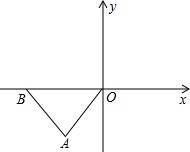 如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)
如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)(1)请用含a的代数式表示△ABO的面积;
(2)若a满足关系式(a+4)2≤0,且以点A、B、O为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点C的坐标
(-12,-4)或(4,-4)或(-4,4)
(-12,-4)或(4,-4)或(-4,4)
;(3)在(2)的条件下,是否存在x轴上的点M(x,0),使△ABM的面积是△ABO的面积的2倍?若存在,求出点M的坐标;若不存在,请说明理由.
(4)在(2)的条件下,请你直接写出y轴上的点N的坐标
(0,24)或(0,-24)
(0,24)或(0,-24)
,使△AON的面积是△ABO的面积的3倍.分析:(1)由A点坐标得到△ABO边OB上的高为|a|,则可根据三角形面积公式计算△ABO的面积;
(2)根据非负数的性质得到a=-4,则A点坐标为(-4,-4),再分类:当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位;当把AB向左平移8个单位,即把点A(-4,-4)向左平移8个单位;当把AB向右平移4个单位,再向上平移4个单位,即把点B(-8,0)向右平移4个单位,再向上平移4个单位;然后写出C点坐标;
(3)根据三角形面积公式得到
×|x+8|×4=2×
×4×8,然后解方程求出x即可得到M点坐标;
(4)设N点坐标为(0,t),根据三角形面积公式得到
×|t|×4=3×
×4×8,解得t=24或-24,然后写出N点坐标.
(2)根据非负数的性质得到a=-4,则A点坐标为(-4,-4),再分类:当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位;当把AB向左平移8个单位,即把点A(-4,-4)向左平移8个单位;当把AB向右平移4个单位,再向上平移4个单位,即把点B(-8,0)向右平移4个单位,再向上平移4个单位;然后写出C点坐标;
(3)根据三角形面积公式得到
| 1 |
| 2 |
| 1 |
| 2 |
(4)设N点坐标为(0,t),根据三角形面积公式得到
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)S△ABO=
×8×|a|=4|a|=-4a;
(2)∵(a+4)2≤0,
∴a+4=0,即a=-4,
∴A点坐标为(-4,-4),
以点A、B、O为顶点画平行四边形,第四个顶点C的坐标为(-12,-4)或(4,-4)或(-4,4);
(3)存在.
×|x+8|×4=2×
×4×8,解得x=8或-24,
∴M(-24,0)或(8,0);
(4)N(0,24)或(0,-24).
故答案为(-12,-4)或(4,-4)或(-4,4);(0,24)或(0,-24).
| 1 |
| 2 |
(2)∵(a+4)2≤0,
∴a+4=0,即a=-4,
∴A点坐标为(-4,-4),
以点A、B、O为顶点画平行四边形,第四个顶点C的坐标为(-12,-4)或(4,-4)或(-4,4);
(3)存在.
| 1 |
| 2 |
| 1 |
| 2 |
∴M(-24,0)或(8,0);
(4)N(0,24)或(0,-24).
故答案为(-12,-4)或(4,-4)或(-4,4);(0,24)或(0,-24).
点评:本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△=
×底×高.也考查了坐标与图形性质、图形平移.
| 1 |
| 2 |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目