题目内容
如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为 .


75°
【考点】平行线的性质.
【分析】首先根据CD∥AB,可得∠A=∠ACD=65°;然后在△ABC中,根据三角形的内角和定理,求出∠ACB的度数为多少即可.
【解答】解:∵CD∥AB,
∴∠A=∠ACD=65°,
∴∠ACB=180°﹣∠A﹣∠B
=180°﹣65°﹣40°
=75°,
即∠ACB的度数为75°.
故答案为75°.
【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确两直线平行,内错角相等,此题还考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.

某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月份,每件配件的原材料价格均比去年10月上涨8元,人力成本比去年增加1元,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少8a%.这样,该月完成了17万元利润的任务,请你计算出a的值.


2011年北京春季房地产展示交易会期间,某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查,共发放100份问卷,并全部收回.统计相关数据后,制成了如下的统计表和统计图:
消费者年收入统计表
| 年收入(万元) | 4.8 | 6 | 9 | 12 | 24 |
| 被调查的消费者数(人) | 10 | 50 | 30 | 9 | 1 |
请你根据以上信息,回答下列问题:
(1)补全统计表和统计图;
(2)打算购买住房面积小于100平方米的消费者人数占被调查人数的百分比为 ;
(3)求被调查的消费者平均每人年收入为多少万元?


设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.


(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a﹣r<d<a+r | |
| d=a﹣r | |
| d<a﹣r |
所以,当r<a时,⊙O与正方形的公共点的个数可能有 个;
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a |
所以,当r=a时,⊙O与正方形的公共点个数可能有 个;
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
 a.
a.



 B.
B.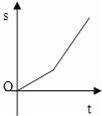


 D.
D.





 )2015 C.(2
)2015 C.(2
