Question

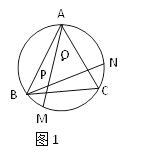
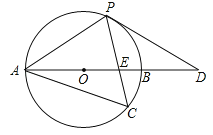
【题目】如图，PA与⊙O相切于点A，AB是⊙O的直径，在⊙O上存在一点C满足PA＝PC，连结PB、AC相交于点F，且∠APB＝3∠BPC，则＝_____．

Answer 1

【答案】．

【解析】

连接OP，OC，证明△OAP≌△OCP，可得PC与⊙O相切于点C，证明BC=CP，设OM＝x，则BC＝CP＝AP＝2x，PM＝y,证得△AMP∽△OAP，可得：，证明△PMF∽△BCF，由可得出答案.

解：连接OP，OC.

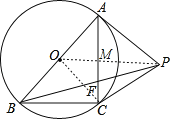
∵PA与⊙O相切于点A，PA＝PC，

∴∠OAP＝90°，

∵OA＝OC，OP＝OP，

∴△OAP≌△OCP（SSS），

∴∠OAP＝∠OCP＝90°，

∴PC与⊙O相切于点C，

∵∠APB＝3∠BPC，∠APO＝∠CPO，

∴∠CPB＝∠OPB，

∵AB是⊙O的直径，

∴∠BCA＝90°，

∵OP⊥AC，

∴OP∥BC，

∴∠CBP＝∠CPB，

∴BC＝CP＝AP．

∵OA＝OB，

∴OM＝．

设OM＝x，则BC＝CP＝AP＝2x，PM＝y，

∵∠OAP＝∠AMP＝90°，∠MPA＝∠APO，

∴△AMP∽△OAP，

∴．

∴AP2＝PMOP，

∴（2x）2＝y（y+x），

解得：，（舍去）．

∵PM∥BC，

∴△PMF∽△BCF，

∴＝．

故答案为：．